|
Chaos and Correlation Artificial Intelligence System for Identification of Social Categories of Natives Based on Astronomical ParametersEugene Lutsenko (Russia), Alexander Trunev (Canada)
The cognitive simulation of AstroDatabank records by using the Artificial Intelligence System – AIDOS, is reviewed in this paper. The technology of simulation is described and the mostly important results are discussed.
Keywords: Semantic Information Models, astrodatabank, Astronomical and Sociological Databases, Neuron-net Training, Numerical Experiment.
IntroductionNew method of identification of a birth chat based on system-cognitive analysis and on the advanced information theory [1] was developed recently [2-3]. This method differs from the normal astrological models so that the birth chat is not interpreted, but it is identified by using a number of attributes and categories, by comparing with the astrological database [4-5], which includes a description of the many key events in real life of real persons. As a result of the identification each person receives a customized description contains classes and categories of events, indicating the likelihood of their implementation. In this research not used any astrological interpretation or any astrological rules. Statistical patterns and the correlation revealed in the data processing of the artificial intelligence system by comparing birth charts and biography. Test examples demonstrate the effectiveness of the system for the recognition of certain classes of entities. Input DatabasesThe main source of astrological database prepared for the artificial intelligence system simulation is the original (first version) Lois Rodden's AstroDatabank [4] and AstroDatabank v. 4.0 [5]. These databases contain biography of famous and ordinary people so that all the categories and events of life are classified and ordered. Data imported from AstroDatabank v. 4.0 were converted into a DBF4 format database. Only 9897 records have been utilized including 5 categories shown below with corresponding number of records: Table 1: Four classes, 5 categories and related number of records
Note, 184 records are repeated among 9897 since they related to 2, 3 or 4 categories listed above. Records were cooperated in four classes as shown in Table 1. Every record has 23 active numerical cells consist of coordinates of celestial bodies, Ascendant and Midhaven at the moment of birth and in the place of birth, i.e.: · Longitude (degree) of the Sun, the Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto, North Node, Ascendant and Midhaven; · Declination (degree) of the Sun, the Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto. From this database were derived two databases to study a declination effect on the similarity parameter: 1. Database1 with 23 active numerical cells in every of 9897 records as described above but all Declination parameters were adapted to the longitude interval (0; 360) by using formula: Declination1 = (Declination +30)*6; 2. Database0 with 23 active numerical cells in every of 9897 records as described above, but all Declination parameters were recalculated as follows: Declination0 = Declination *0, also for all records we put Ascendant= Midhaven =0, therefore only Longitude of the Sun, the Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto and North Node have been utilized in this database. After this minor adaptation all 23 cells have one scale and format, therefore they could be analyzed in the same manner as well as the declination parameter effect on the simulated outcomes could be studied. The data imported from original Lois Rodden's AstroDatabank were converted into the Borland JDataStore format databases. Then, the data were sorted using SQL queries and special functions written in Java. Only 20007 records related to 1931 categories and events have been utilized in this research. For these records were calculated coordinates of celestial bodies (latitude and longitude in degrees, and the distance in astronomical units). 12 cusps of astrological houses in the Placidus system were calculated for records with the exact time of birth. The ephemeredes following celestial bodies and points were established: the Sun, the Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto, and North Node. The next step is sorting by category of records. As result XML tree categories reference database was obtained. Next, the database has been completely exported in Excel and then it converted to the DBF4 format (which accepted by the artificial intelligence system). Only 23 active numerical cells in every of 20007 records were utilized in this research, i.e.: Longitude (degree) of the Sun, the Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto, North Node, and 12 cusps of the astrological houses (houses in the Placidus system). From this database were derived several databases: 1. Database A of 20007 records related to 500 representative categories (category represented in the database at least 26 times); 2. Database B of 15007 records related to 500 representative categories - training data set; 3. Database C of 5000 records which are not used in the Database B (but used in the Database A) – recognized data set. 4. Database D of 20007 records related to 240 unrepresentative categories (number of records related to category higher than 2 and less than 25) – low frequency limit; 5. Database E of 20007 records related to 870 categories (number of records related to any category higher than 2) – mostly complete database; 6. Database F of 20007 records related to 37 categories (number of records related to any category higher than 1000) – higher frequency limit; 7. Database F1 of 20007 records related to 100 categories (number of records related to any category higher than 174); 8. Database G of 20007 records related to 4 categories listed below in Table 2, b. In this database 8150 records are not involved in a simulation. Table 2: Four classes, four categories and related number of records in a case of Database G
Note 20007 records are related to the original (first version) Lois Rodden's AstroDatabank [4] and AstroDatabank v. 4.0 [5] as well. The difference between these databases is that latest version updated with more than 5000 records, and it is a reason why the same category SPORT has different records in Table 1 and 2. The Model and the Artificial Intelligence System - AIDOSAs well know there are several ways to decompose Zodiac circle in a process of analyzing a birth chart: · day and night houses partition – 2 sectors; · Cardinal signs, fixed and mutable signs – 3 multiply connected sectors. · squares – 4 sectors; · partition based on element of fire, earth, air and water – 4õ3 sectors; · zodiac signs – 12 sectors; · decants – 36 sectors; · terms – 60 sectors; · Degree – 360 sectors. Decomposition combinations such as those listed above seem to resemble algorithms of grid simulation widely used in a modern science, in which condensation of the grid helps improve convergence in solving the task. We utilized this method in order to perform packet recognition of 9897 or 20,007 records exported from AstroDatabank and presented as DBF4 format databases. In order to do this a solution founded based on data from 172 grids of various dimensions, containing 2, 3, 4, ..., 173 sectors consequently (it is a limit for this task at the moment). Thus the net entropy effect could be established during this simulation with the system of artificial intelligence AIDOS [2]. Standard AIDOS package includes 7 subsystems and 85 programmable applications organized in a block structure – see Table 1. Generally speaking it is a neuron-net computer application running under Windows XP in MS-DOS mode, designed with CLIPPER 5.01, Tools-II and BiGraph 3.01, provided the following objectives: 1. Synthesis and adaptation of the semantic data model. 2. Identification and forecasting. 3. Precise analysis of the semantic data model. Table 3: Generalized Structure of the Universal Cognitive Analytical System AIDOS, v. 12.03.2008
The cognitive simulation of AstroDatabank records including the neuron-net training and recognition was realized for any grid of fixed dimension N=2, 3, 4…, 173 sectors. Thus there are many models – M2, M3, M4… M173 corresponding to the number of sectors in a given partition of Zodiac. For every model could be established own catalog (they are numbered simply as 002, 003, 004 …) and a copy of the system AIDOS. To manage the input parameters and outcomes of all models a special system has been designed [3], which would be implemented "collectives decisive rules» i. e., would the ability to automatically generate a number of models that would form one coherent system, which called "multi-model". This system consists of few programmable applications which allow setup any combination of models; run the neuron-net training and recognition for all models, organize and summarize the results of the identification of the respondents in different models for a set of categories. Main ResultsThe technology of simulation described in papers [6-8]. In fact the system AIDOS operates with Object Code like numbers in a left column in Tables 1, 2. Astronomical parameters also have own code called “scale or graduation code”, for instance, in a case of model M3 we have 23 main scales and 69=23*3 graduations; six of them shown below:
If any record in a training database shows a longitude of the Sun belongs to the interval (0.000, 120.000) then a frequency of the corresponding code 1 increases on a unit. Therefore a frequency of scales in the training database could be calculated and the frequency matrix and the information matrix could be established. For example, in a case of model M2 trained with Database F, a fragment of the frequency matrix and a fragment of the information matrix are shown in Table 4a and 4b consequently:
Table 4a: The frequency matrix (fragment) in a case of model M2 trained with Database F (frequency is given in absolute value) [7]
Actually an information counted in the system with 8 decimal places, but in Table 4b it shown with 2 decimal position (*100) only. A positive or negative value of information in a cell ij in Table 4b means that category j has a positive or negative correlation with scale i.
Table 4b: The information matrix (fragment) in a case of model M2 trained with Database F (information given in Bit*100) [7]
When a training of the neuron-net for every model is finished, then packet recognition could be run. It starts from definition of recognized sample records number. In a case of Database0, Database1 or Database G with 4 classes only a reasonable number could be N=400 or 100 per class. The trained computer neuron-net has a reaction on any input data which are similar to the training sample. Therefore every record from N could be analyzed and four possible reactions on it could be measured:
Thus the effective artificial intelligence system should be designed in a way to minimize a false prediction and to maximize a true prediction. For the best understanding of the packet recognition results a special form of the similarity parameter has been proposed as follows [7]:
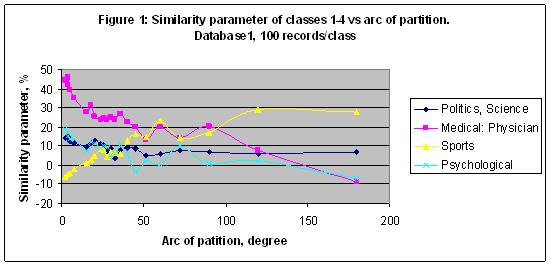
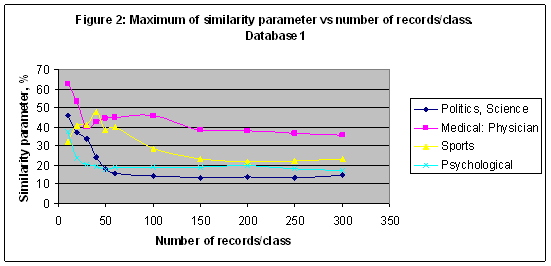
With this definition the similarity parameter changes from -100% up to 100%, like a statistical correlation parameter. If Sm=0, it means that the category number m is not recognized well even if BTnm =0.95 for every true record and it looks like a very good result. From the other side if Sm=0.5, it is really a good result even if BTnm =0.5 for every true record, but it means that there are no false records and every true record been recognized. Let conduct few experiments to recognize several categories. EXPERIMENT 1 In the first experiment the multi-model of 22 models including M2, M3, M4, M5, M6, M7, M8, M9, M10, M11, M12, M13, M14, M15, M18, M20, M24, M48, M72, M90, M96, M150 was setup and then 22 models were trained with Database1 of 9897 records. As result an information image (portrait) of every class has been simulated. Similarity parameters of classes 1-4 (series 1-4) from Table 1 versus the arc of partition (degree) in a case of packet recognition 100 records/class are shown in Figure 1. The number of records effect on the similarity parameter shown in Figure 2, where data for the maximum of the similarity parameter are plotted.
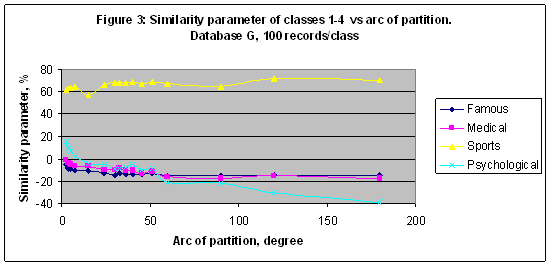
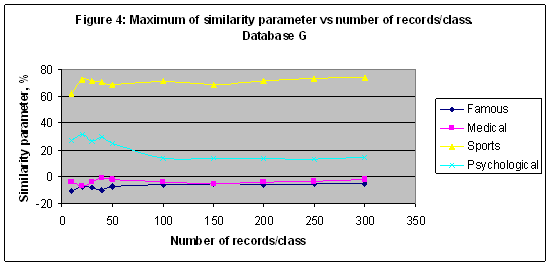
In the first experiment the best result obtained for the category “Medical: Physician” - S= 45.908% in a case of model M90 and for 100 records/class. Reducing a number of records/class it is possible to increase a similarity parameter of the category “Medical: Physician” up to 62.722 in a case of model M150 and for 10 records/class – see Figure 2. For the category “Sport” the best result S= 47.526% was found in a case of model M4 for 40 records/class. Note that it is less than a random choice probability = 0.609478 for this category. Nevertheless, a similarity parameter reflects a response of the artificial intelligence system on the astronomical parameters effect on the training and recognition while a random choice probability is a fixed value for a fixed database, and it depends on the number of records only. EXPERIMENT 2 In the second experiment all simulations of the first experiment have been repeated with Database G of 20007 records – see Figures 3-4. In this experiment the best recognized category is “Sport” with S= 72.273 in a case of model M3 and for 100 records/class.
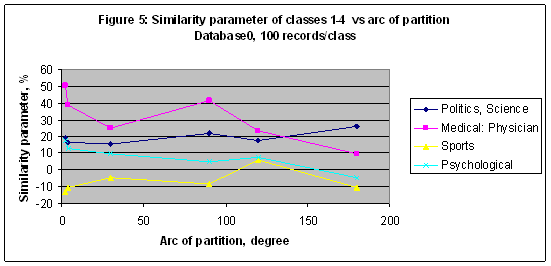
EXPERIMENT 3 In the third experiment the multi-model of 6 models including M2, M3, M4, M12, M90, and M150 was established and trained with Database0 (9897 records). Similarity parameters of classes 1-4 (series 1-4) from Table 1 versus the arc of partition (degree) in a case of packet recognition 100 records/class are shown in Figure 5. There is a big difference in the final results for two databases – Database1 and Database0 (see Figure 1 and Figure 5); even they have identical number of records, but different number of scales – 23 (longitude and declination of 10 planets, longitude of North Node, Ascendant and MC) and 11 (longitude of 10 planets and North Node only) consequently. In this experiment the best result was found for the category “Medical: Physician” - S= 50.634% in a case of model M150, and it is comparable with data shown in Figure 1. For the category “Sport” the best result is S=5.915% in a case of model M3, and it is much less than S=28.935% found for this category in a case of Database1 and model M3 – see Figure 1.
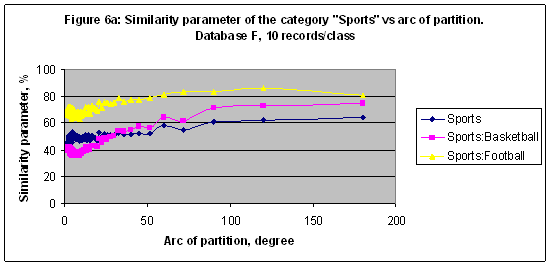
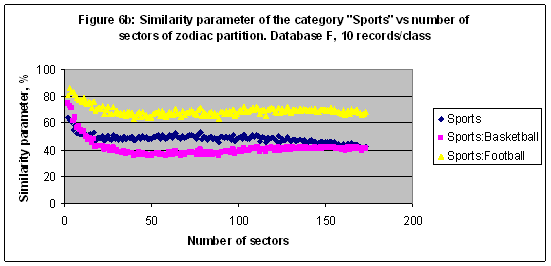
EXPERIMENT 4 In the fourth experiment the multi-model of 172 models including M2, M3, M4, …, M172, and M173 was established and trained with Database F (20007 records) [7]. With this model it is possible to run a precise simulation for those categories which been decomposed in several subcategories or classes. For instance, the similarity parameter of the category “Sports” decomposed in three classes (see Table 5) shown in Figures 6a, 6b versus arc of partition and number of sectors of zodiac circle partition consequently. The best result S= 85.864 found for the subcategory “Sports: Football” in a case of model M3. Table 5: The category “Sports” decomposed in three classes and related numbers of records. Database F
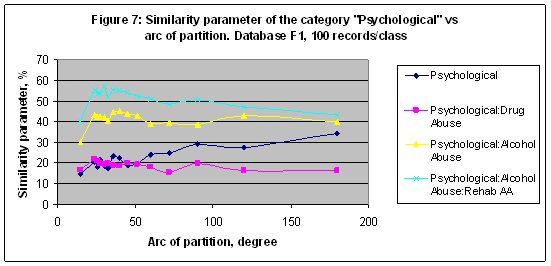
EXPERIMENT 5 In this experiment the multi-model of 15 models including M2,M3,M4,M5,M6,M7, M8,M9,M10,M11,M12,M13,M14,M15,M24 was established and trained with Database F1 (20007 records). The similarity parameter of the category “Psychological” decomposed in four classes – see Table 6, shown in Figure 7. The best result S= 57.244 found for the subcategory “Psychological: Alcohol Abuse: Rehab AA” in a case of model M12. Note that subcategories mostly showed better results in recognition than a main category. Table 6: The category “Psychological” decomposed in four classes and related numbers of records. Database F1
EXPERIMENT 6 In this experiment the model M12 only has been setup and trained with Database B of 15007 records. Then all records from Database C have been utilized for recognition. In result the number of the true recognized records was determined as Ntrue=3435 or 68.7% of 5000 records [6]. To compare this result with some background data the stochastic Database of 5000 records has been generated (all the active sell numbers taken from a random set) the same size and format as Database C, and recognized, finally a maximum of the similarity parameter has been established as Smax=1.206% [6]. Therefore a value of the similarity parameter which is higher than 1.206 * 2.5 = 3.015 % should be considered as a certain value with 95% probability. This criterion was taken into account in the simulation with records of Database C.
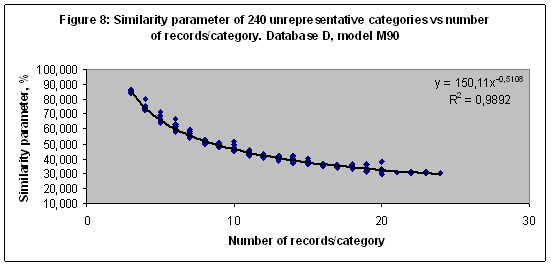
EXPERIMENT 7 In seven experiment the multi-model of 4 models including M3, M4, M12 and M90 was setup and trained with Database D of 20007 records related to 240 unrepresentative categories (number of records related to category higher than 2 and less than 25). The similarity parameter of 240 categories versus the number of records related to every category in Database D in a case of the model M90 shown (together with a trend line) in Figure 8. These data illustrate the low frequency trend in a case of the recognition, when the number of records for any category is not statistically representative.
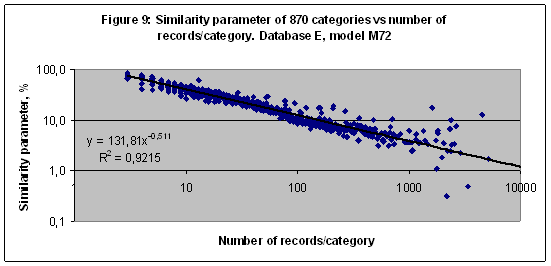
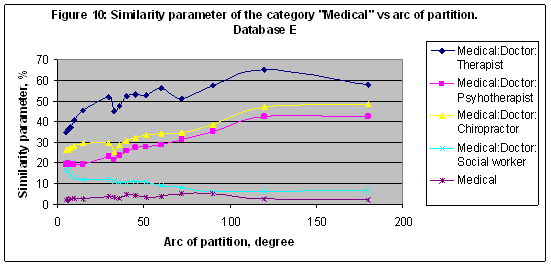
EXPERIMENT 8 In this experiment the multi-model of 16 models including M2,M3,M4,M5,M6,M7, M8,M9,M10,M11,M12,M24,M36,M48,M60 and M72 was established and trained with Database E (20007 records and 870 categories). The similarity parameter of 870 categories versus the number of records related to every category in Database E in a case of the model M72 shown (together with a trend line) in Figure 9 (there is a double logarithmic scale performed). The trend line in this case has the same slope like in Figure 8 therefore it could be a common correlation for 20007 records utilized in both databases - D and E. The similarity parameter of the category “Medical” and several subcategories (see Table 7) are shown in Figure 10. The best result S=65.109 found for the subcategory “Medical: Doctor: Therapist” in a case of model M3.
Table 7: Category “Medical”, subcategories and related number of records
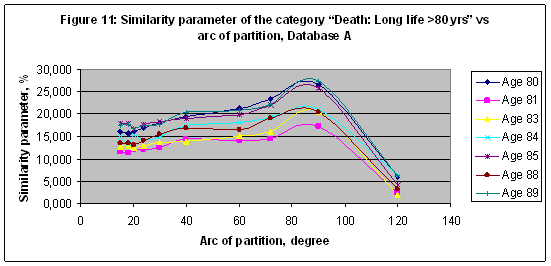
EXPERIMENT 9 In this experiment a multi-model of 10 models including M3,M4,M5,M6,M9, M12,M15,M18,M20,M24 was trained with Database A of 500 representative categories (category represented in the database at least 26 times). The similarity parameter of the category “Death: Long life >80 yrs”, and several subcategories (see Table 8) are shown in Figure 10. The best result S=27.504 found for the subcategory “Age 89” in a case of model M4. Note that all subcategories data shown in Figure 11 have synchronic behavior versus the arc of partition. . Table 8: Category “Death: Long life >80 yrs”, subcategories and related number of records
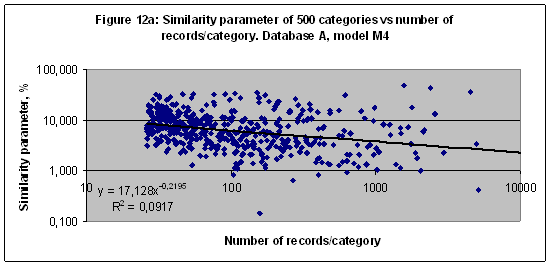
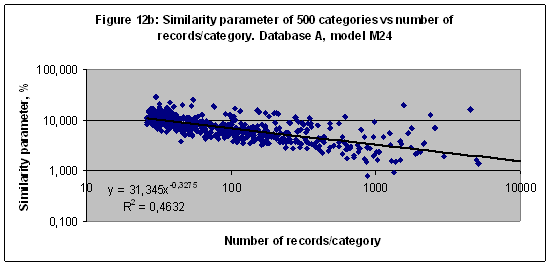
Net entropy effect on the similarity parameterThe similarity parameter of 500 categories versus the number of records related to every category in Database A in a case of the model M4 shown (together with a trend line) in Figure 12a. These data look like chaotically dispersed points. There is a dramatic difference between data in Figures 9 and Figure 12. It should be noted that both databases A and E have same numbers of records per category but there are different numbers of scales in models M72 and M4 which depend on number of sectors. Therefore it is possible to increase a correlation by increasing number of scales - see Figure 12b. It calls the net entropy effect.
In Figure 12c the average similarity parameter of 37 categories versus number of sectors is shown [7]. These data could be approximated by the logarithmic function – a solid line in Figure 12c. The function of entropy (or information) also depends on the number of elements as a logarithmic function [1]. Thus the average similarity parameter is a linear function of the net entropy (or information as well). Nevertheless some categories better recognized at the small number of sectors – see Figure 6b for instance. DiscussionSeveral databases have been tested with the artificial intelligence system AIDOS to found out the astronomical parameters effect on the social categories of natives. The data of the multi-model simulations shown in Figures 1-12c demonstrate a regular respond of the similarity parameter on variations of the number of records per class or category as well as on the arc of zodiac cycle partition. Therefore the astronomical parameters effect on the social categories of natives could be investigated and determined as it has been performed above. An information portrait is the main astronomical characteristic of any category. For instance, the category “Sports” in a case of Database F1 and model M12 could be characterized as follows (only 62 scales of 276 are shown):
It is impossible to derive any simple suggestion like “category Sports depends on the Pluto or Mars position” from this portrait only. Generally speaking any information portrait depends on the utilized model and database. Nevertheless it gives some ideas about predominate scales in the information portrait of the category Sport. Note that every scale contributes a portion of information which actually utilized for recognition. Every recognized record has own similarity portrait, for example, the portrait of the record for Bush, George Walker could be presented as follows:
In this table the similarity parameter of the category “U.S. Presidents” is 22% only. It is because the category “U.S. Presidents” was recognized with a maximum of the similarity parameter 19.376% in a case of Database E and model M72. Thus George W Bush looks similar to 41 U.S. Presidents with a relative probability 22/19.376= 1.135 or 113.5%. He also looks similar to other categories from this table, for instance, to the category “Taxi driver”. But in this case a relative probability is 74.7% and 3 records only (“Taxi driver” is an unrepresentative category in this database). The similarity portrait could be used for a prediction of the social status of native. To increase a probability of this prediction several algorithms have been developed and verified [3, 7-8]. Test examples demonstrate the effectiveness of the system for the recognition of chats of respondents. References
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||