|
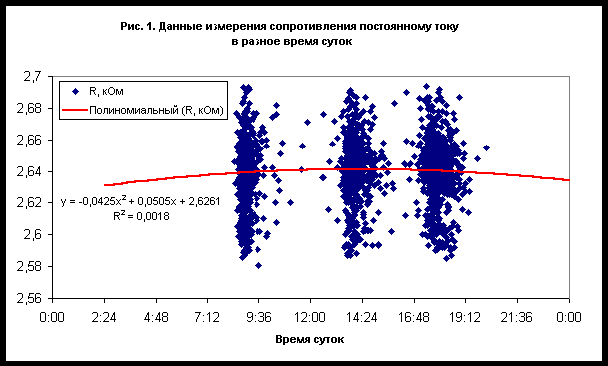
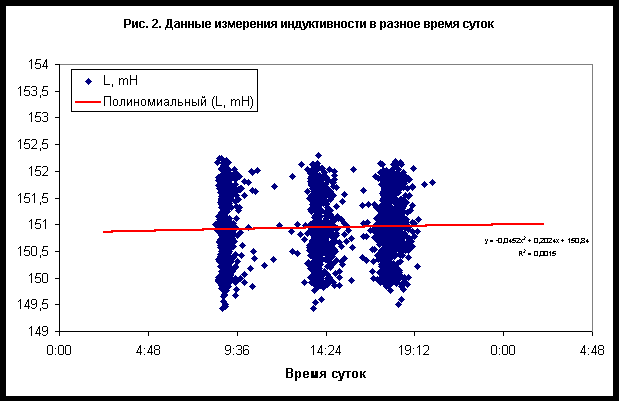
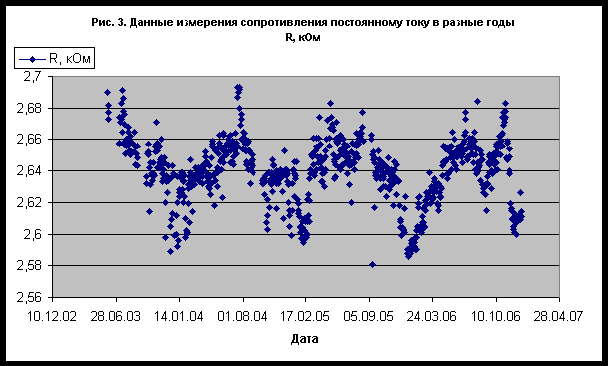
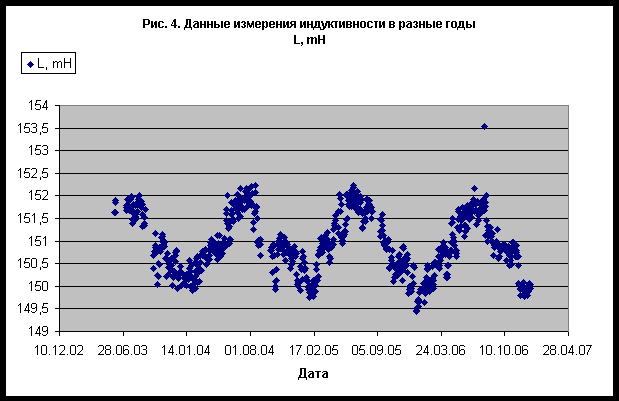
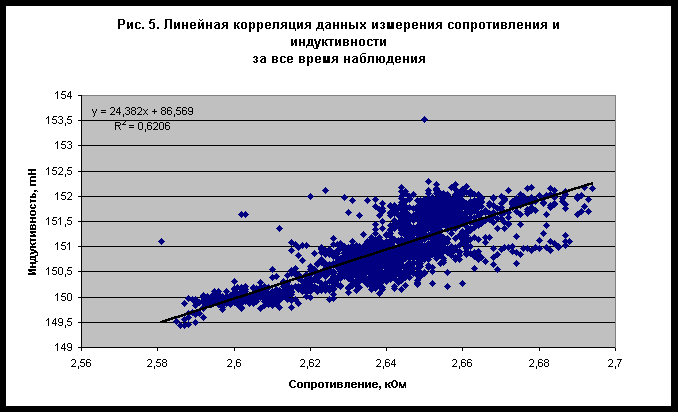
Chaos and Correlation О влиянии небесных тел Солнечной системы на электрические и магнитные свойства материаловAlexander P. Trunev (Toronto, Canada)В работе /1/ была высказана гипотеза о влиянии гравитационных полей небесных тел Солнечной системы на электрические и магнитные свойства материалов. Для доказательства своей гипотезы авторы /1/ использовали экспериментальные данные многолетних измерений сопротивления постоянному току и индуктивности. В качестве прибора использовался электрический мост для измерения сопротивления электрической цепи в случае постоянного и переменного тока при фиксированной температуре окружающей среды. Ряды наблюдений, сделанных в разное время суток на протяжении несколько лет демонстрируют изменение параметров сопротивления и индуктивности, синхронное совокупному движению планет Солнечной системы. Авторы /1/ не выполнили статистическую проверку своей гипотезы, поэтому высказанная ими идея о влиянии гравитационных полей на электрические и магнитные свойства материалов можно рассматривать как рабочую гипотезу, которая нуждается в дальнейшей проверке. Используя данные /1/, можно проверить степень выполнения гипотезы о влиянии движения планет Солнечной системы на ряды измерений сопротивления электрической цепи постоянному и переменному току при постоянной температуре окружающей среды. При этом сама природа влияния остается под вопросом. Первичный анализ данныхДанные /1/ были получены на установке по измерению сопротивления участка электрической цепи, представляющую собой мост марки М, помещенный в термостат при постоянной температуре 20C. Замеры производились 1-3 раза в сутки, совокупность данных для сопротивления постоянному току приведена на рис. 1, а для индуктивности - на рис. 2. Данные, полученные за все время наблюдений, представлены на рис. 3-4. Эти данные показывают отчетливую сезонную зависимость. Следует заметить, что средняя суточная вариация измерений невелика. Можно предположить, что максимум сопротивления постоянному току наблюдается около 2 часов дня, а максимум индуктивности - около 2 часов ночи. Однако параметр достоверности аппроксимации данных невелик, R 2=0,0018 для сопротивления и R2=0,0015 для индуктивности, поэтому можно считать, что суточные вариации данных за все время наблюдений практически отсутствуют. С другой стороны, сезонная вариация данных сравнительно велика - см. рис. 3-4, поэтому может служить предметом для дальнейшего изучения.Чтобы удостовериться в том, что сезонные вариации сопротивления постоянному току и индуктивности вызваны сходными факторами, достаточно сравнить ряды данных этих величин за все время наблюдения - рис. 5. Параметр достоверности аппроксимации линейной корреляции сопротивления и индуктивности за все время наблюдения составляет R 2=0,6206. Очевидно, что статистический критерий достоверности гипотезы о взаимосвязи вариаций сопротивления и индуктивности не выполняется. Это можно объяснить, например, нелинейными эффектами и магнитными явлениями, от которых зависит индуктивность. Вообще следует заметить, что данные по индуктивности представляются более однородными, а данные по сопротивлению более размытыми - см. рис. 3-4. Поэтому следует ожидать, что корреляция с движением планет является более выраженной для индуктивности, нежели для сопротивления постоянному току.
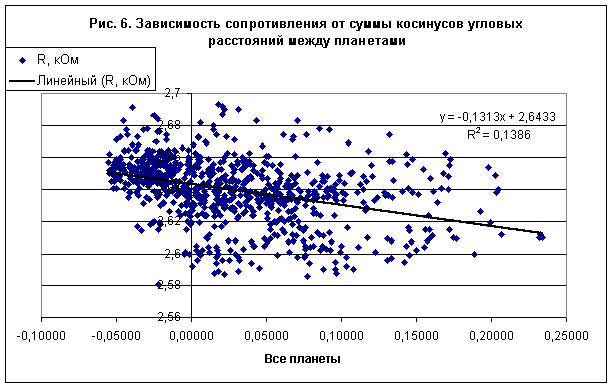
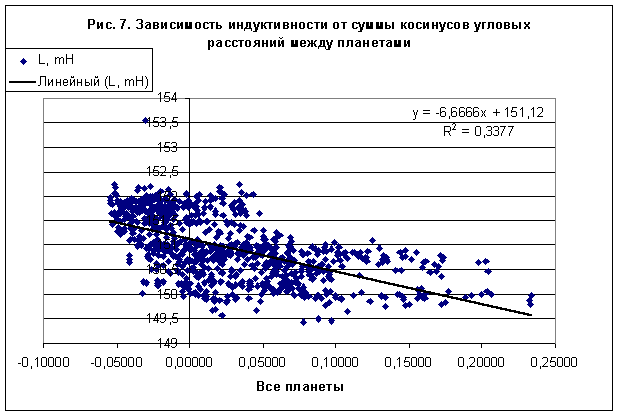
Взаимосвязь сезонной вариации данных и динамики планет Солнечной системыДинамику планет Солнечной системы можно характеризовать одним скалярным параметром, в качестве которого можно взять, например, сумму косинусов угловых расстояний между планетами, взятыми в объеме с весовыми коэффициентами /2/. Это параметр является некоторым аналогом конфигурационной энтропии /3/. Были исследованы зависимости рядов данных измерений сопротивления и индуктивности, полученных в 2003-2006 гг, от суммы косинусов угловых расстояний между планетами, взятыми с единичными коэффициентами - рис. 6, 7. Как и следовало ожидать, параметр достоверности аппроксимации линейной связи (данных измерения) сопротивления с параметром, характеризующим динамику Солнечной системы, имеет низкое значение R 2=0,1386, тогда как в случае данных по индуктивности аналогичный параметр составляет R2=0,3377 - рис. 7. Это означает, что, либо магнитные свойства материалов в большей степени подвержены влиянию планет, нежели электрические свойства, либо реакция индуктивности является более прямой и быстрой, нежели реакция сопротивления.
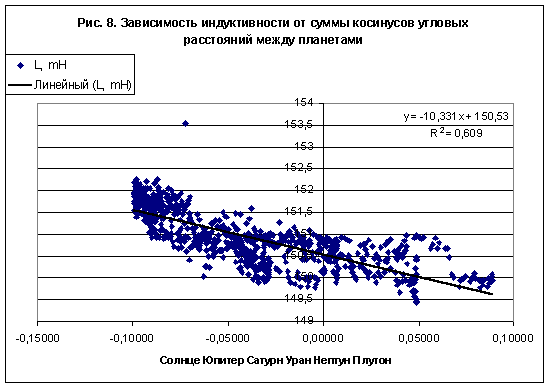
Чтобы повысить достоверность аппроксимации, из суммы косинусов угловых расстояний между планетами были исключены члены, характеризующие положение быстрых и малых небесных тел - Луны, Меркурия, Венеры и Марса, но сохранены слагаемые, характеризующие положение Солнца, Юпитера, Сатурна, Урана, Нептуна и Плутона - рис. 8. В результате параметр достоверности аппроксимации линейной корреляции индуктивности с параметром, характеризующим положение планет Солнечной системы, повысился и составил R 2=0,609, а для сопротивления аналогичный параметр повысился более чем в 2,5 раз и составил R2=0,3576. Заметим, что если планеты-гиганты Юпитер, Сатурн, Уран и Нептун действительно могут вызвать заметное возмущение гравитационного потенциала /4-6/, то роль Плутона не столь понятна. Возможно, влияние Плутона объясняется тем, что в 2006 году Плутон находился в знаке Стрельца в непосредственной близости от центра Галактики, который тоже вносит вклад в возмущение гравитационного потенциала, соизмеримое с влиянием Урана и Нептуна, благодаря годичному вращению Земли /6/.
Были проверены различные комбинации планет, с целью выявления степени влияния отдельных факторов на сезонное изменение индуктивности (сопротивления). Некоторые результаты представлены в Таблице 1. Первая комбинация - угловой аспект Венеры и Юпитера. Ранее было установлено /4/, что Венера и Юпитер оказывают заметное влияние на годичное изменение гравитационного потенциала. Достоверность аппроксимации в этом случае очень низкая - R 2= 0,0003 (0,0002 для сопротивления), что указывает на отсутствие какой-либо корреляции с аспектом этой пары планет.Вторая комбинация - это внешние планеты: Марс Юпитер Сатурн Уран Нептун Плутон. Как оказалось, линейная связь сезонных изменений индуктивности с положением внешних планет является довольно слабой, в этом случае R 2= 0,1216 (0,0322). Следовательно, определяющую роль играет Солнце в комбинации с внешними планетами, а не внешние планеты сами по себе (третья комбинация).Третья комбинация - Солнце и внешние планеты: Марс Юпитер Сатурн Уран Нептун Плутон. В этом случае R 2= 0,3332 (0,1453), что подтверждает высказанную выше гипотезу о решающем вкладе Солнца.Четвертая комбинация - это все планеты, но ее влияние не самое сильное, видимо из-за быстрого движения Луны. Действительно, если исключить Луну (шестая комбинация), тогда достоверность аппроксимации заметно возрастает. Достоверность аппроксимации сравнима со случаем третьей комбинации. Пятая комбинация - Меркурий Венера Марс Юпитер Сатурн Уран Нептун Плутон, т.е. основные планеты, кроме Солнца и Луны, дающие заметный вклад в изменение гравитационного потенциала. Для этой комбинации параметр достоверности аппроксимации R 2= 0,4391 (0,1868).Шестая комбинация включает все планеты, кроме Луны. Достоверность аппроксимации в этом случае заметно выше, чем в комбинации всех планет, R2= 0,4985 (0,2321).Седьмая комбинация - это все планеты без вклада Луны, Меркурия и Марса. Эта комбинация выбрана только для сравнения с седьмой комбинацией. В этом случае R 2= 0,5978 (0,3333).Наконец, восьмая комбинация это все планеты, кроме Луны, Венеры, Марса и Меркурия (т.е. кроме быстрых планет). Линейная связь сезонных вариаций индуктивности с положением планет этой комбинации имеет самую высокую достоверность аппроксимации, R 2= 0,6090 (0,3576). Заметим, что в этом случае достоверность аппроксимации можно повысить еще на 20%, если использовать нелинейную функцию, например, полином четвертой степени.Во всех случаях достоверность аппроксимации линейной корреляции данных замеров сопротивления заметно ниже, чем для индуктивности.
Таблица 1. Параметр достоверности аппроксимации линейной корреляции индуктивности (сопротивления) и параметра, характеризующего положение различных комбинаций планет Солнечной системы
Обсуждение результатовВ настоящее время не существует какой-либо теории, объясняющей полученный результат о связи сопротивления и индуктивности с параметром, характеризующим относительное положение планет Солнечной системы. Можно выдвинуть две гипотезы:
Первая гипотеза может быть отвергнута на основании данных Таблицы 1, из которых следует, что достоверность аппроксимации возрастает при изменении комбинации планет в сторону последней комбинации, содержащей Солнце и группу медленных планет - Юпитер, Сатурн, Уран, Нептун и Плутон. Если бы связь была случайной, тогда любая комбинация из 8 могла бы иметь максимальное значение параметра достоверности аппроксимации. Но максимальную достоверность имеет именно та комбинация, которая могла бы проявиться при наличии взаимодействия, зависящего от расстояния. Действительно, расстояние до внешнего небесного тела можно определить через расстояние от земли до Солнца, расстояние от небесного тела до Солнца и через угловой аспект небесного тела к Солнцу по формуле: (1) Здесь Для группы медленных планет, находящихся на большом удалении от земли, выражение (1) можно упростить и представить в виде: (2) где многоточие соответствует упущенным более высоким членам разложения по малому параметру отношения Для точно круговых орбит (или для малых, по сравнению с периодом обращения небесного тела, промежутков времени) уравнение (2) дает однозначную связь между расстояние от земли до небесного тела и угловым расстояние между небесным телом и Солнцем. Медленные же планеты отличаются тем, что угловые расстояния между ними меняются незначительно за период в 1 год. Потому основной вклад в изменение сумму косинусов угловых расстояний между планетами дает обращение Земли вокруг Солнца. Таким образом, в случае медленных внешних планет наличие корреляции сезонной вариации индуктивности (сопротивления) с суммой косинусов угловых расстояний между планетами равносильно корреляции с расстоянием от земли до планеты.С этой точки зрения становятся понятными результаты, приведенные в Таблице 1. Например, комбинация внешних планет (№2) при добавлении Солнца превращается в комбинацию №3, которая имеет такую же достоверность аппроксимации, как и комбинация, включающая все планеты (№4 ). Такой же эффект наблюдается при добавлении Солнца в комбинацию №5, в результате чего получается комбинация №6. Но добавление Солнца равносильно учету расстояния от земли до небесных тел, участвующих в комбинации.Следовательно, полученные результаты однозначно свидетельствуют, что связь сезонных вариаций индуктивности (сопротивления) с параметром, характеризующим положение планет, не является случайным, но обусловлено неким фактором, зависящим от расстояния между нашей планетой и другими небесными телами Солнечной системы. С целью доказательства этого утверждения нами были изучены зависимости сезонных вариаций индуктивности и сопротивления от расстояния до небесных тел в случае аппроксимации данных линейной функцией - таблица 2 , и степенной функцией - таблица 3. Как оказалось, наиболее достоверной является зависимость от расстояния до Солнца, Сатурна, Урана, Нептуна и Плутона. Самой слабой является связь данных с расстоянием до Луны и Марса. Меркурий, Венера и Юпитер составляют группу планет, для которых связь, видимо, существует, но настолько мала, что ею можно пренебречь.Таблица 2. Зависимость сезонных вариаций индуктивности и сопротивления от расстояния до небесных тел Солнечной системы в случае аппроксимации линейной функцией. В ячейках указаны параметры функции и (или) достоверность аппроксимации (здесь и ниже, в таблицах 3-4, R2=R2).
Таблица 3. Зависимость сезонных вариаций индуктивности и сопротивления от расстояния до небесных тел Солнечной системы в случае аппроксимации степенной функцией. В ячейках указаны параметры функции и достоверность аппроксимации.
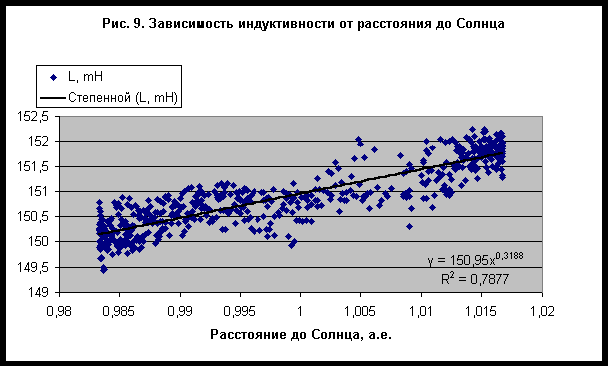
Обнаруженные связи не являются однотипными. Так, зависимость сезонных вариаций индуктивности и сопротивления от расстояния до Солнца и Сатурна является прямой, а для Урана, Нептуна и Плутона наблюдается обратная зависимость. Это объясняется тем, что основной вклад в изменение расстояния до планеты вносит вращение Земли вокруг Солнца. Поэтому зависимость от расстояния до Солнца, которая является самой достоверной из всех, отражается, согласно уравнению (1) на зависимости от расстояния до планеты. Причем в наибольшей степени это влияние проявляется для планет, находящихся вблизи оси Рак-Козерог (в данном случае Плутон и Сатурн), а в наименьшей степени для планет, находящихся вблизи оси Овен - Весы (в этом случае Юпитер). Заметим, что экспериментальные данные были собраны в период со 2 июня 2003 года по 29 декабря 2006 года. Для большой серии данных Сатурн находился в знаке Рака (с 3 июня 2003 по 16 июля 2005), поэтому для него наблюдается прямая зависимость, как для Солнца (отметим, что Земля максимально удалена от Солнца, когда Солнце находится в знаке Рака). Плутон все это время находился в последних градусах знака Стрельца, близко от оси Рак-Козерог, поэтому для него наблюдается обратная зависимость. Эту связь между расстоянием до Солнца и планеты можно легко обнаружить путем линейной аппроксимации - таблица 4. Таблица 4. Линейная аппроксимация зависимости между расстоянием до планеты и расстоянием до Солнца. Указаны параметры функции и достоверность аппроксимации.
Найденная зависимость индуктивности от расстояния до Солнца - рис. 9, не позволяет однозначно утверждать, что эта зависимость возникает благодаря влиянию гравитационного потенциала (например, на энергию активации физических процессов в твердых телах по механизму, описанному в работах /5-6/). Можно лишь утверждать, что такая зависимость существует и что она является прямой, как в случае сезонных вариаций индуктивности, так и для сопротивления. Неясно, почему на эти вариации не оказывает влияния Луна, ведь ее гравитационное поле вызывает заметные на глаз приливы и отливы. Сложно интерпретировать и влияние других планет Солнечной системы из-за указанной взаимосвязи расстояний до небесных тел. Тем не менее, сам факт наличия такой зависимости позволяет по-новому взглянуть на проблему измерения в земных лабораториях, в которых следует принимать в расчет сезонную вариацию электротехнических параметров.
БлагодарностиАвтор выражает благодарность Татьяне Черноглазовой за предоставленные экспериментальные данные и полезные обсуждения.Ссылки |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||