|
Chaos and Correlation О зависимости проводимости и намагниченности материалов от гравитационного потенциала Солнечной системы©Alexander P. Trunev (Toronto, Canada)В работе /1/ на основе экспериментальных данных /2/ была получена зависимость сезонных колебаний индуктивности и сопротивления от расстояния до Солнца. В настоящей работе дана теория этого явления. Согласно классической теории Друде-Лоренца, проводимость металлов зависит от числа электронов проводимости по формуле: (1) где При комнатной температуре число электронов проводимости определятся для данного материала уровнем энергии Ферми /3/: (2) Энергию Ферми, в свою очередь, можно связать со средней энергией, приходящуюся на один электрон: (3) Здесь Во внешнем гравитационном поле общая энергия частиц изменяется на величину (4) где (5)
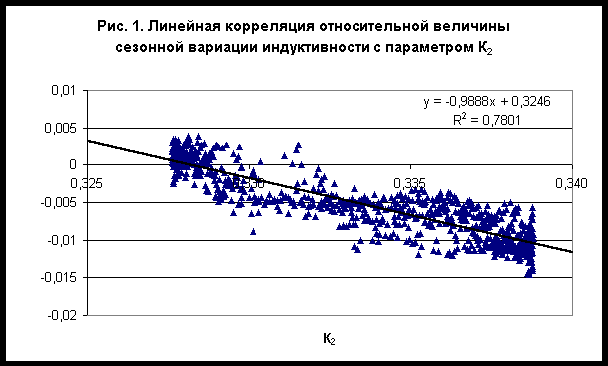
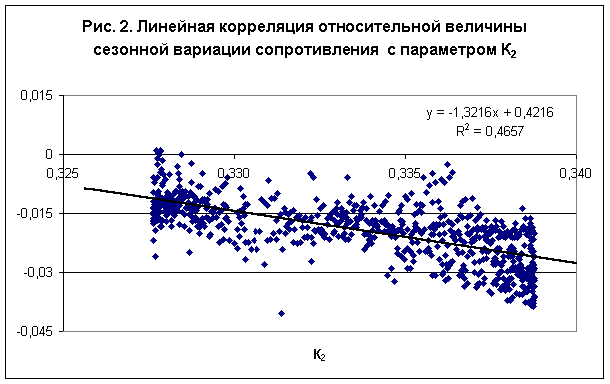
При фиксированном числе частиц изменение энергии приводит, согласно (3), к пропорциональному изменению энергии Ферми: (6) Как известно, распределение свободных электронов по энергиям описывается статистикой Ферми-Дирака /3/: (7) На верхнем уровне при (8) Если уровень энергии Ферми испытывает колебания в соответствии с (6), тогда на верхнем уровне имеем: (9) Вычитая из этого уравнения выражение (8), находим изменение плотности функции распределения на уровне (10) Составим два безразмерных комплекса: (11) где Первый из этих комплексов характеризует относительный вклад изменения уровня энергии Ферми в сезонные вариации электрических и магнитных свойств материалов в соответствии с выражением (2), второй комплекс характеризует статистические эффекты, обусловленные температурой окружающей среды согласно (10). Используя теорему о размерностях, относительный эффект сезонного изменения электрического сопротивления или индуктивности можно представить в форме: (12) где При фиксированной температуре окружающей среды параметры Экспериментальные данные /1/ по сезонным вариациям электрического сопротивления и индуктивности можно обобщить линейными зависимостями в виде: (13) Таким образом, установлено, что и сопротивление и индуктивность электрической цепи, измеренные по мостовой схеме при постоянной температуре Т=293,15К, изменяются прямо пропорционально величине суммарного гравитационного потенциала Солнечной системы. Из выражений (13) следует, что этот эффект имеет статистический характер, т.е. обусловлен влиянием температуры окружающей среды. Дадим объяснение полученным результатам. Возмущение плотности функции распределения (10) порождает пропорциональное возмущение плотности свободных электронов. Поскольку масштаб энергии в этой задаче соответствует уровню энергии Ферми, возмущение плотности можно представить в виде (14) где a - численный коэффициент.Возмущение плотности электронов проводимости вызывает пропорционально изменение проводимости согласно (1), а относительное изменение сопротивления описывается линейным уравнением: (15) Экспериментальные результаты (13) позволяют вычислить неизвестный численный коэффициент:
Отрицательное значение этого коэффициента означает, что энергия Ферми уменьшается в гравитационном поле в полном соответствии с выражением (6). Аналогичный эффект может быть получен и для намагниченности. Так, в случае парамагнетизма металлов имеем для вектора намагниченности /3/: (16) где Из выражений (2), (6) и (14) следует, что магнитная восприимчивость пропорциональна величине гравитационного потенциала, т.е. возрастает в ночное время (при максимальном удалении от Солнца) и убывает днем, что и было обнаружено экспериментальным путем в работе /2/. Наконец заметим, что изложенная выше модель расчета возмущения уровня энергии Ферми применима не только в случае классической теории Друде-Лоренца, но и в случае квантовой теории. Действительно, и в классической и в квантовой теории предполагается, что проводимость пропорциональна плотности числа свободных электронов, но в квантовой теории вместо массы электрона в правой части выражения (1) фигурирует эффективная масса, обусловленная рассеянием электронов на примесях и тепловых колебаниях решетки. Кроме того, данную модель можно применить для расчета проводимости в любых внешних полях, изменяющих энергию свободных электронов в соответствии с уравнением (4).
Ссылки |

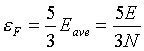
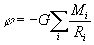 .
. 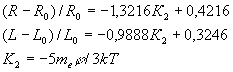
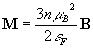
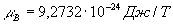 - магнетон Бора,
- магнетон Бора,