|
Chaos and Correlation Алгоритмы и законы типизации и идентификации субъектов по астрономическим данным на момент рождения©Евгений Луценко (Краснодар, Россия)©Александр Трунев (Торонто, Канада)©Владимир Шашин (Санкт-Петербург, Россия)
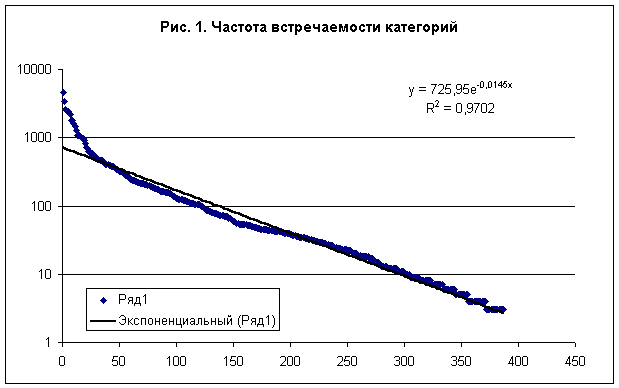
В работах /1-2/ описан математический метод идентификации субъектов по астрономическим данным на момент рождения, который фактически является альтернативой для обычной натальной астрологии. Суть метода заключается в том, что на основе анализа базы данных рождения, категорий и событий жизни множества реальных субъектов, формируется описание категорий и событий, содержащее связи между астрономическими параметрами. Данный подход отличается от обычной астрологии тем, что при распознавании образов используются корреляционные связи, которые выявляются путем многокритериальной типизации респондентов обучающей выборки по исследуемым категориям. При этом на этапе синтеза модели рассчитывается количество информации, которое содержится в фактах попадания долгот углов в интервалы (рассматриваемые как критерии), о принадлежности респондента к тем или иным категориям, а на этапе идентификации эта информация используется для расчета степени сходства конкретных респондентов с обобщенными категориями. В работах /3,4/ был предложен алгоритм распознавания на 19 сетках различного масштаба для смешанной БД содержащей 500 категорий. В настоящей работе выполнено исследование моделей с целью определения наиболее эффективного алгоритма идентификации и типизации для профессиональной БД содержащей 387 категорий на 12 сетках различного масштаба. 1. Статистические закономерности идентификацииВходные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. Общее число категорий, определенное для исследуемой БД составляет 1907 (первоначально справочник категорий включал 10988 категорий /2/), а число исследуемых случаев равно 192879, т.е. примерно 9,64 случая на одного респондента. В настоящей работе для повышения достоверности идентификации из списка категорий были отобраны только те из них, которые соотносятся с профессиями. Полученный список профессиональных категорий содержит только 387 наименований (см. Приложение 1), которые представлены в исходной БД с разной частотой встречаемости - рис. 1. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) - прямая сплошная линия на рис. 1. Суммируя все частоты, находим общее число исследуемых случаев N= 69742. Учитывая, что в исходной БД содержится только 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=3,49. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона. Поскольку модель является дискретной, координаты долготы задавались на 12 сетках различного масштаба с числом секторов разбиения 3, 4, 5, 6, 9, 12, 15, 18, 20, 24, 36, 72 соответственно.
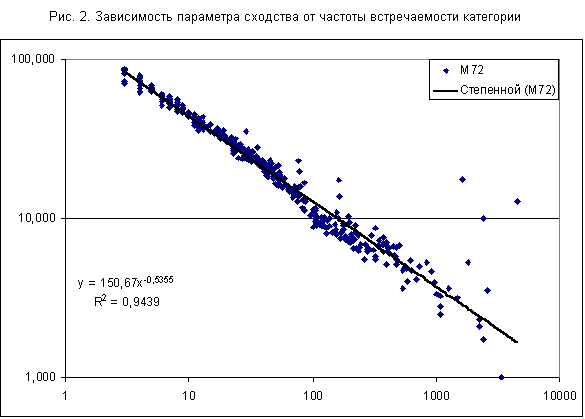
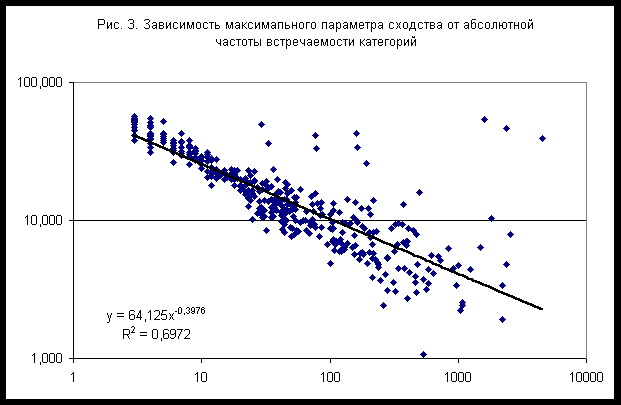
При исследовании частных моделей были установлены некоторые статистические закономерности распознавания, позволяющие повысить эффективность моделей. Во-первых, во всех частных моделях наблюдается обратная зависимость параметра сходства от частоты встречаемости категории: чем выше частота, тем ниже параметр сходства. На рис. 2 представлены результаты распознавания категорий в модели с 72 секторами. В этом случае зависимость параметра сходства от частоты описывается степенной функцией с показателем степени b=-0,5355. Аналогичная зависимость наблюдается и для максимального по всем моделям параметра сходства - рис. 3 (на рисунках 2-3 по горизонтальной оси дана абсолютная частота, т.е. общее число случаев данной категории).
Во-вторых, параметр сходства зависит от числа секторов разбиения - см. таблицу 1А. Все категории можно разбить на три класса в зависимости от величины частоты встречаемости и поведения параметра сходства при изменении числа секторов разбиения. Первый класс составляют категории, для которых параметр сходства убывает с ростом числа секторов разбиения, как это было обнаружено ранее в работах /3,4/. Этот класс категорий характеризуется высокой частотой встречаемости при высоком уровне распознавания, что соответствует данным, лежащим выше линии корреляционной зависимости на рис. 2-3. Некоторые категории этого класса приведены в таблице 1Б вместе с корреляционными зависимостями параметра сходства от числа секторов разбиения. Отметим, что в работах /1-4/ была исследована БД, содержащая 500 категорий преимущественно первого класса. Поэтому была получена обратная зависимость среднего параметра сходства от числа секторов /3,4/. Второй класс составляют категории, для которых параметр сходства возрастает с ростом числа секторов разбиения. Этот класс категорий характеризуется низкой частотой встречаемости и относительно высоким параметром сходства, что соответствует данным, группирующимся вблизи линии корреляционной зависимости на рис. 2-3. Большая часть исследуемой в настоящей работе БД представлена категориями этого класса, поэтому средний параметр сходства возрастает с ростом числа секторов - рис. 4. Отметим, что в современной натальной астрологии используется именно этот класс категорий, поэтому для повышения вероятности распознавания широко применяется анализ на множестве сеток, полученных при разбиении круга Зодиака вплоть до градусов и минут. Третий класс составляют категории, для которых параметр сходства изменяется немонотонно с ростом числа секторов разбиения. Как правило, эти категории имеют среднюю частоту встречаемости и относительно небольшую величину параметра сходства. Общее их число невелико в исследуемой БД, поэтому они не оказывают существенного влияния на поведение среднего параметра распознавания. Таблица 1Б. Категории первого класса, их абсолютная частота встречаемости и корреляционная зависимость параметра сходства от числа секторов разбиения.
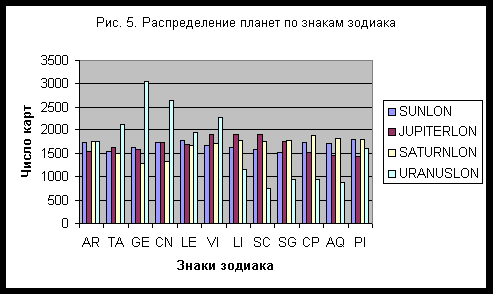
Насколько представительной является исследуемая БД и какое поколение в ней представлено? Только 2576 карт принадлежат людям, родившимся до 1901 года, остальные родились в 20 веке вплоть до 1998 года включительно 2. Режимы голосования моделейДля обработки результатов пакетного распознавания на множестве сеток в работе /3/ был предложен алгоритм, который в данной работе был дополнен еще четырьмя алгоритмами, для выбора наиболее эффективного из них. Таким образом, сравнивались пять алгоритмов, получивших общее название РЕЖИМЫ ГОЛОСОВАНИЯ МОДЕЛЕЙ:
Сравнение осуществлялось следующим образом. Согласно первому алгоритму выбирался список распознанных категорий, определялось их число, а затем по 4 другим моделям выбирался список с таким же числом категорий, распознанных наилучшим образом по данному алгоритму. В таблице 2 дан пример такого сопоставления. Таблица 2. Сопоставление категорий, распознанных по 5 алгоритмам.
Путем сопоставления номеров категорий можно определить те из них, которые присутствуют во всех пяти моделях. В данном случае это 18 категорий, собранных в таблице 2. Таблица 2. Категории, опознанные в пяти моделях и упорядоченные по параметру сходства первой модели
Поскольку категории в таблице 2 распознаются по всем пяти алгоритмам, все пять алгоритмов можно считать эквивалентными в смысле определения множества категорий из таблицы 2. Различие же алгоритмов может проявиться в установлении приоритетности категорий. Например, категория 165 (SC:B781-Law:Police/Security) распознается по первому алгоритму как наиболее достоверная, по второму алгоритму она оказывается на 4 месте, по третьему - на 7, по 4 - на 15, а по 5 - на 33. С другой стороны, категория 36 (SC:B1330-Sports:Martial Arts), которая распознается по пятому алгоритму с наибольшей достоверностью, также хорошо распознается и по первому алгоритму, но плохо распознается по третьему. Это означает, что каждый из алгоритмов имеет погрешность по отношению к другому, а наиболее эффективным может оказаться алгоритм, являющейся комбинацией указанных выше пяти алгоритмов. Такой комбинацией может быть описанный метод определения пересечения множества категорий, распознанных по каждому алгоритму. Ссылки
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Логотип исследования: в работе изучены 12 частных моделей с разбиением круга зодиака на 3 4 5 6 9 12 15 18 20 24 36 72 секторов.
Каждой частной модели соответствует кольцо. Сектора в частных моделях разных цветов спектра, в данном случае используется 16 цветов.
