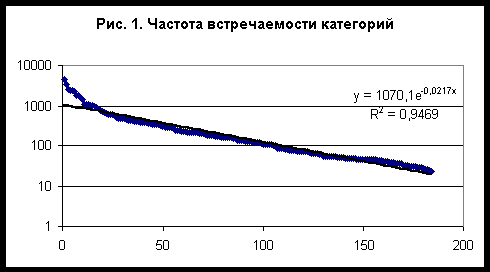
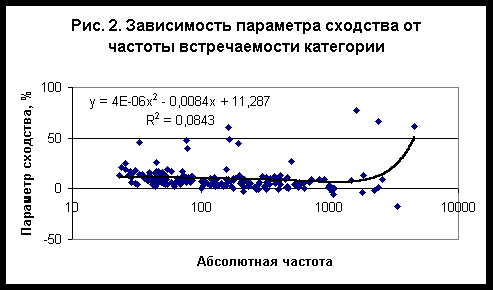
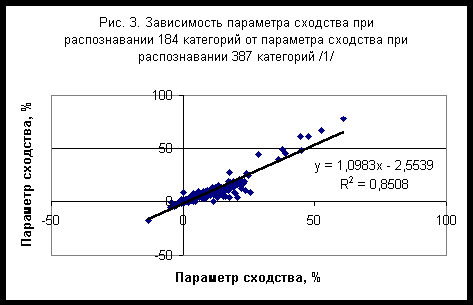
Chaos and CorrelationInternational Journal, No 8, July 18, 2007Метод разделения категорий в задаче типизации и идентификации субъектов по астрономическим данным на момент рождения©Евгений Луценко (Краснодар, Россия)©Александр Трунев (Торонто, Канада)©Владимир Шашин (Санкт-Петербург, Россия)В работе /1/ выполнено исследование моделей распознавания субъектов по астрономическим данным на момент рождения с целью определения наиболее эффективного алгоритма идентификации и типизации для профессиональной базы данных (БД) содержащей 387 категорий на 12 сетках различного масштаба. Было установлено, что категории можно разбить на три класса в зависимости от поведения параметра сходства от числа секторов. К первому классу были отнесены категории, для которых параметр сходства убывает с ростом числа секторов. Ко второму классу относятся категории, у которых параметр сходства возрастает с ростом числа секторов, а к третьему классу - категории, у которых параметр сходства ведет себя немонотонно. Логично предположить , что если отобрать категории первого класса в отдельную базу данных, то для их распознавания достаточно будет сетки из четырех секторов. В данной работе изучен вариант модели распознавания субъектов по астрономическим данным на момент рождения для профессиональной БД содержащей 184 категории первого и третьего класса на сетке из 4-х секторов. Установлено, что для этих категорий параметр сходства практически не зависит от частоты встречаемости категорий в исходной БД, содержащей 20007 данных независимых респондентов. Путем исключения категорий первого и третьего класса из профессионально БД содержащей 387 категорий, была получена база данных категорий второго класса в составе 203 категорий и установлены общие свойства категорий всех классов.Исходные данные и результаты идентификации категорий первого и третьего классаИсходные данные задачи представляют собой таблицу, содержащую 20007 записей (строк) независимых респондентов, каждый из которых характеризуется номером записи, именем, полом, датой и временем рождения, местом рождения, собственной биографией и набором категорий и событий жизни. На основе данных места и времени рождения вычислялись астрономические параметры. В качестве входных астрономических параметров модели использовались координаты долготы углов 12 домов (в системе Плацидуса), Лунных Узлов и 10 небесных тел – Солнца, Луны, Меркурия, Венеры, Марса, Юпитера, Сатурна, Урана, Нептуна, Плутона. Общее число категорий, определенное для исследуемой БД, составляет 1907. Из списка категорий были отобраны те из них, которые соотносятся с профессиями и для которых параметр сходства убывает с ростом числа секторов или изменяется немонотонно. Полученный список профессиональных категорий содержит только 184 наименования (см. таблицу 1), которые представлены в исходной БД с разной частотой встречаемости - рис. 1. Частотное распределение с большой степенью точности описывается экспонентой (распределение Пуассона) - прямая сплошная линия на рис. 1. Суммируя все частоты, находим общее число исследуемых случаев N= 60011. Учитывая, что в исходной БД содержится 20007 данных независимых респондентов, находим среднее число категорий, приходящихся на одну карту, n=N/20007=2,9995.Подробное описание алгоритмов идентификации дано в работах /2-5/. В настоящей работе распознавание осуществлялось на сетке из 4-х секторов, полученных путем деления круга зодиака на 4 части, начиная с нулевого градуса знака Овна. Как оказалось, для отобранных категорий параметр сходства практически не зависит от частоты встречаемости категории - рис. 2, тогда как в аналогичной задаче параметр сходства убывает с ростом частоты /1/. Можно сравнить параметры сходства идентичных категорий в этих двух задачах - рис. 3. Как следует из полученных данных, эти параметры связаны линейной зависимостью, причем параметр сходства при распознавании категорий в составе БД из 184 категорий приблизительно на 10% выше, чем в составе БД из 387 категорий (см. рис. 3). Отсюда следует, что обратная зависимость параметра сходства от частоты /1/, возникает из-за наличия в исследованной в работе /1/ БД 203 категорий второго класса. Эти категории отличаются малой частотой встречаемости, поэтому вероятность их случайного угадывания является крайне низкой. При распознавании категорий этого класса требуется большое число входных параметров, поэтому они хорошо распознаются на сетках с большим числом секторов (число входных параметров задачи пропорционально числу секторов).
Упорядочивая данные таблицы 1 по параметру сходства, можно выделить наиболее хорошо распознаваемые категории первого класса - таблица 2. Среди 32 категорий, приведенных в этой таблице, 8 составляют спортивные категории, 6 - различные бизнесы, 5 - оккультные, 3 - медицинские доктора, 3 - дизайнеры, фотографы и художники, 2 - писатели детективов и фантастики, 2 - игроки, 2 - строители и 1 - экипажи судов, поездов и автобусов. Таблица 2. Список наиболее хорошо распознаваемых категорий первого класса
Плохо распознаваемые категории этого класса приведены в таблице 3. Из 32 категорий этого типа 12 составляют различные знаменитости (!), 6 - наука и образование, 5 - журналисты, писатели и издатели журналов, 2 - политики, 2 - юристы, 2 - музыканты-инструменталисты и по одной категории фермеров, оккультистов и финансистов. Интересно, что если знаменитостей сгруппировать в отдельные категории по характеру получаемой премии, то они попадают во второй класс и распознаются довольно хорошо. Рассмотрим этот вопрос более подробно. Таблица 3. Плохо распознаваемые категории первого класса.
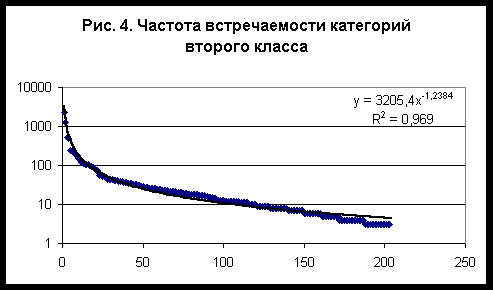
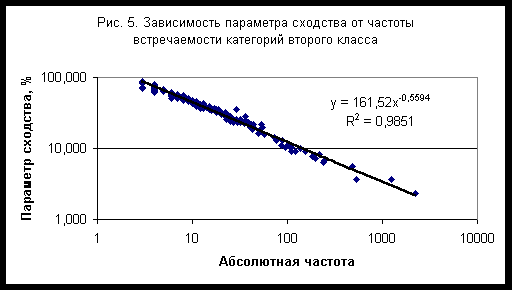
Общие свойства категорий второго классаСписок категорий второго класса, упорядоченных по частоте встречаемости, приведен в таблице 4 вместе с параметром сходства, полученным на сетке, содержащей 72 сектора. Частотное распределение категорий второго класса с большой степенью точности описывается степенной функцией - рис. 4. Зависимость параметра сходства от частоты также описывается степенной функцией - рис. 5. Поскольку вероятность случайного угадывания пропорциональна частоте встречаемости, из этих данных следует, что для второго класса категорий параметр сходства обратно пропорционален вероятности случайного угадывания в степени a=0,5594.
Рассмотрим категорию ЗНАМЕНИТЫЙ ( Famous), разбитую на малые группы по характеру получаемой премии или социальному отличию - таблица 5. Из данных этой таблицы следует, что обладатели редких премий распознаются лучше, нежели обладатели известных, но широко распространенных премий. Становится понятной и закономерность, отраженная на рис. 5. Малочисленные группы в ряду многочисленных групп всегда более заметны, поэтому распознаются лучше. Например, эфиоп на улицах Москвы будет более заметен, нежели в ряду соплеменников на улицах Аддис-Абебы, поэтому его легко будет распознать. С другой стороны, блондин из Москвы, впервые попавший на улицы Аддис-Абебы, немедленно попадет в малочисленную категорию белых людей, поэтому будет легко узнаваем. В этом смысле распознавание в системе искусственного интеллекта АИДОС существенно отличается от простой статистики, в которой главным критерием достоверности является отклонение от генеральной совокупности.Таблица 5. Категория Famous (знаменитый) разбитая на малые группы по характеру премии
При объединении знаменитостей в одну категорию A15-Famous получается довольно многочисленная группа (3372 случая), которая не имеет никаких общих признаков, кроме того, что эти люди знамениты. Поэтому параметр сходства/различия у этой группы имеет значение -16,945, что указывает на неоднородность группы. При разбиении же группы на малые подгруппы с ярко выраженными профессиональными признаками, параметр сходства становится положительным, что указывает на возросшую однородность состава подгрупп. Аналогичный пример дает категория ОБРАЗОВАНИЕ - таблица 6. Малые группы преподавателей, объединенные по специальностям, распознаются на порядок лучше, чем общая категория A108-Education, содержащая 1002 случая (см. таблицу 3). При этом подгруппы общей категории относятся ко второму классу, т.е. хорошо распознаются на сетке из 72 секторов, а общая категория относится к первому классу, т.е. лучше всего распознается на сетке из 4 секторов.Таблица 6. Категория ОБРАЗОВАНИЕ разбитая на малые подгруппы
ОбсуждениеСуществуют категории, например, B173-Sports:Football, которые характеризуют заведомо однородные группы, объединенные по яркому профессиональному признаку. У этой группы самый высокий параметр сходства среди категорий первого класса, несмотря на ее многочисленность (1613 случаев). На втором месте по параметру сходства оказалась группа баскетболистов - см. таблицу 2. Но если объединить футболистов и баскетболистов в одну большую группу СПОРТ, параметр сходства понижается, поскольку группа становится неоднородной. Такие многочисленные однородные по составу группы хорошо распознаются на сетке из четырех секторов. С другой стороны, малочисленные однородные группы хорошо распознаются на сетках с большим числом секторов (в данной работе распознавание осуществлялось на сетке, включающей 72 сектора). На первый взгляд кажется, что признаки малочисленных профессиональных групп не могут быть использованы для тестирования, поскольку не выполнены статистические критерии достоверности. На самом же деле критерий сходства отличается от стандартных критериев достоверности, типа критерия Стьюдента. Критерий сходства хорошо иллюстрирует следующий пример. Предположим, что у нас есть база данных, включающая 20007 фотографий известных людей. Мы хотим протестировать фотографии неизвестных людей, чтобы выяснить, на кого они более всего похожи внешне. У нас есть интеллектуальная система, которая позволяет отобрать из БД насколько десятков фотографий и расставить их по параметру сходства. При этом оказывается, что на одних фотографиях схожесть достигается за счет формы носа, на других за счет овала лица, на третьих за счет разреза глаз и т.д. Заменим теперь фотографии на карты рождения, включающие описание астрономических параметров, социальных и психологических категорий. Задача распознавания при этом не изменилась, но на выходе мы получим набор категорий, характеризующих тестируемого субъекта. Если при этом субъект оказался похож на малочисленную профессиональную категорию, то это нельзя назвать простым совпадением. Ведь совпадение с малочисленной группой маловероятно. Кроме того, путем прямых экспериментов доказано, что вероятность распознавания по астрономическим данным на момент рождения в сотни раз превосходит вероятность случайного угадывания /2/. Следовательно, полученные результаты так или иначе могут быть отнесены к числу характеристик субъекта, но при этом необходимо помнить, что сходство и подобие не означает тождество.Заметим, что первые эксперименты по идентификации и типизации субъектов по астрономическим данным на момент рождения были выполнены на смешенной базе данных, содержащей 500 социальных (профессиональных) и личностных (в т.ч. психологических) категорий /4-5/. Для повышения уровня параметра сходства и достоверности идентификации была образована новая база данных, содержащая только 387 социальных (профессиональных) категорий /1-2/. Полученные с ее помощью результаты отличаются высокой степенью достоверности идентификации. Рассмотренный в настоящей работе метод позволяет повысить параметр сходства путем разделения категорий на классы , не увеличивая числа входных параметров задачи.Ссылки |