Applied Mathematics
Model of aerosols turbulent transport
The mathematical models of
the turbulent transport of aerosols in the atmosphere are based mainly on the
hypothesis that the eddy diffusivity for the small-sized particles is
proportional to the eddy diffusivity of a heat and the latter value is assumed
proportional to the eddy viscosity. In turn the turbulent eddy viscosity in the
stratified flows is determined from the empirical formulas or from the k-e model, or from
the turbulent kinetic energy model.
Turbulent
boundary layer model also can be developed for the case of the atmospheric
aerosols transport. This model based on the viscous heat-conducting gas
transport equation and on the dynamical model of the dust cloud. The aerosol is considered as sets of identical, small-sized particles,
which move chaotically under influence of thermal fluctuations and are involved
in macroscopic movement together with the airflow. The mass concentration of
aerosol particles is considered so small, that the influence of particles to
gas dynamic can be neglected. The dynamic parameters of the aerosol particles
can be averaged to exclude of the chaotic thermal motion, then its can be
described by the continuous functions: the numerical concentration and the
aerosol particles flow velocity. Thus at the description of aerosol dynamics we
shall take into account the Brownian diffusion, weight and inertia of
particles. The motion of mono-disperse small particles in a dust cloud are
governed by the transport and momentum equations:
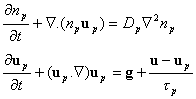
where np
is the particles numerical density, up is the particles flow
velocity vector, Dp is the particle diffusion coefficient.
The
diffusion coefficient of the small particles is given by the Einstein's
formula: 
, where k=1.38*10-23J/K is the Boltzmann
constant, mp is the particle mass, tp is the time relaxation parameter which for the spherical particles in
the Stokes' regime is given by 
, dp is
the particle aerodynamic diameter, rs is the particle material density.
Utilized
the transformation method explained in the books [1,2], one can derive the
equation system for the aerosol turbulent transport in the case when the
aerosol particles are formed due to the condensation from the vapor phase as
follows
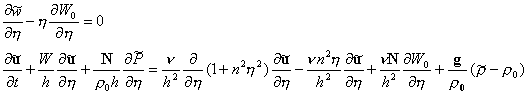
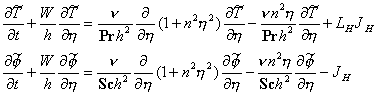
where
are the random
function of the particles flow velocity and numerical density, accordingly; 
is the vertical
turbulent transport rate of aerosol, 
, 
is the particles turbulent kinetic energy in the small volume
, 
is the Schmidt number of aerosol, 
is the latent
heat, 
is the rate of
the phase transition which depends on the air temperature and vapor pressure
as 
, here 
is the gas
constant of the vapor phase.
References
Trunev A. P. Theory of Turbulence and Turbulent Transport in the Atmosphere. WIT
Press, 2001.
Trunev A. P. Theory
of Turbulence, Russian Academy of Sciences, Sochi, 1999.
Trunev,
A. P., Similarity theory and model of turbulent dusty gas flow over large-scale
roughness, Abstr. of Int. Conf. On Urban
Air Quality: Monitoring and Modelling, University of Hertfordshire,
Institute of Physics, London, p. 3.8, 1996.