ОПЫТ АСТРОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ ЕЖЕДНЕВНЫХ РЯДОВ ТЕМПЕРАТУРЫ и ОСАДКОВ
А. Бударовский (Симферополь)
www.astrolcrimea.nm.ru
Очень часто можно встретить утверждение, что температура и осадки хорошо
коррелируют с фазами Луны. Х. С.
Грин в своей широко известной работе [2] писал (гл.3)
«Когда Солнце и Луна почти
одновременно аспектируют какую-либо планету, что время от времени происходит в
новолуние, полнолуние или четверти, влияние этой планеты на погоду чувствуется
очень сильно, поскольку аспекты светил усиливают друг друга.
Существует широко
распространенное мнение, что изменение погоды происходит с большой вероятностью
в новолуние, но астрономы часто указывали, что статистика не подтверждает эту
идею и использовали этот факт как аргумент против влияния Солнца и Луны на
погоду.
С точки зрения астрометеорологии и это мнение, и спор против него основываются на неправильном понимании. Влияние на погоду оказывают не Солнце и Луна, а любая планета, с которой эти светила образуют аспекты приблизительно одновременно; такое может случаться в новолуние, полнолуние или в четверти, как уже было сказано, но может случаться и в другое время, что подтвердит взгляд в эфемериды, и когда бы такое ни происходило, будет ощущаться влияние данной планеты. Даже если такое происходит в новолуние, совсем не обязательно в следующее новолуние будет что-то другое; на самом деле если планета, о которой идет речь, движется медленно, например, это Уран, светила могут оказаться в квадратуре к ней вблизи времени одного новолуния и в секстиле или трине к ней же в следующее новолуние, и тогда эффекты будут подобными.
Лунные аспекты, образуемые в то
время, когда Луна находится на экваторе, на тропиках или в крайнем склонении,
особенно сильны и важны, как и солнечные аспекты в этих положениях.
Издавна известно, что Полная
Луна имеет склонность разгонять облака и давать чистое небо.
В среднем больше дождя бывает, когда Луна растет, чем когда она убывает, и больше во время второй четверти, чем в любое другое время».
В работе [3] я приводил сравнение временных характеристик фаз Луны и естественных синоптических
периодов. Повторим основные положения. Во многих работах метеорологов (например, [4]) подтверждается
существование циклов погоды, называемых «естественные синоптические периоды»
(ЕСП). Длительность ЕСП 4.5 - 5.5 суток или другими
словами, некоторая барическая система (циклон или антициклон) существует в среднем 5 суток. Она может существовать
от 9 до 11 суток. Тогда длительность ее жизни равна 2 ЕСП. Очень трудно
подобрать соответствующий астрологический фактор. Связь с циклами Луны, которые вроде бы
можно приспособить к оправданию ЕСП, сомнительна, т.к. лунная фаза занимает 7
суток. В то же время, существование и длительность ЕСП не подвергается сомнению
и установлена многими исследованиями. С течением времени ЕСП все более уходит
от моментов лунных фаз, но совпадает с лунным циклом в периодах, близких к 15 и
30 дням, создавая иллюзию влияния Луны на погоду. Лявуа в [4], подтверждая это
положение пишет: «Благодаря исследованию и
предсказанию погоды я понял, что действие карты новолуния длится только до
первой четверти Луны.»
Данные утверждения Грина и Лявуа могут быть проверены экспериментально.
Все на самом деле просто. Нужно взять достаточно длинный ряд измерений
температуры, произведенных в одном месте и определить существующие тренды. Что
было и сделано автором. Рассмотрим методику и результаты
1. Материал и методика
1.1
Температура
Чего только нельзя найти в Интернете? Пожалуй, все. И
температурные ряды тоже. Правда, искал я долго. Поиски, наконец, увенчались
успехом. На одном из сайтов обнаружились ежедневные ряды температуры и осадков
для достаточно большого интервала времени (около 40 лет), что обеспечивает
необходимую статистику. Так как живу я в Крыму, то и станцию выбрал самую
близкую – Джанкой.
С исходными данными нужно было что-то делать. Методик для обработки
существует великое множество, вплоть до спектрального анализа временных рядов.
Но, нужен был такой метод, который позволил бы решить следующие проблемы:
Ø
Избавиться от
сезонного хода температур,
Ø
Рассматривать
временные интервалы вблизи полнолуния или новолуния.
Ø
Был простой и
имел достаточную степень достоверности.
Именно таким методом является давно известный и очень простой метод
«наложенных эпох», который разработал в 1913 году английский магнитолог Кри. Он
изучал 27-дневную ритмичность возмущений магнитного поля Земли. Этот метод был
применен Лявуа и Тарасовым в [1]. Коротко
опишем основу метода.
Исследователь должен иметь в свом распоряжении ежесуточные значения какого-либо
индекса, например, температуру. Прежде всего выбираются дни, являющиеся
реперными. В нашем случае это – новолуния. Будем называть их - нулевые. Отложим от каждого из нулевых дней в
обе стороны некоторое число дней N и выпишем для них
значения индекса. Расположим в таблице значения так, чтобы все нулевые дни были расположены друг под другом столбцом.
Произведем усреднение по всем столбцам и получим некоторую кривую, которая
возможно будет указывать на существование ритма.
Для
того, чтобы избавиться от сезонного хода температур, модернизируем метод Кри
следующим образом: сначала для каждого ряда найдем разницу между температурой в
+/- N день и нулевой. Таким образом, мы
нормализуем каждую строчку
относительно температуры в день новолуния и сезонные колебания температуры при
усреднении столбцов уже не имеют значения.
Анализировались
значения температуры и осадков для
210 новолуний. От нулевого дня в обе стороны откладывались значения температуры
по 14 дней, т.е. до следующего полнолуния. Данные приведены на рис.1
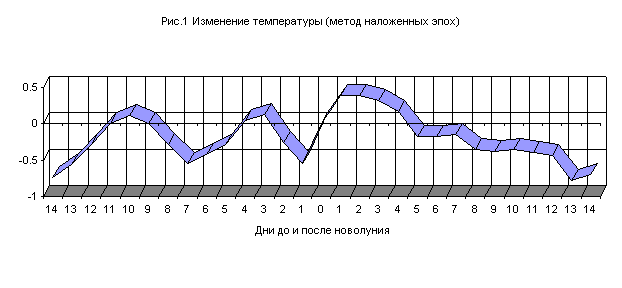
На рисунке 1 видно, что на новолуние температура имеет тенденцию к
подъему, а на полнолуние – к падению. Максимальное значение наступает на +1
день, т.е. на следующий день после новолуния. Причем, падение температуры от
новолуния к полнолунию, на растущей Луне плавное, в районе 1 четверти есть
плато. Также перелом наступает в районе третье четверти (-7 день). К сожалению, приходится констатировать,
что ошибки, рассчитываемые по общепринятым формулам статистики достаточно
большие (от 2 до 5 градусов). Так что с точки зрения статистики полученный нами
график есть прямая линия, все изменения в пределах ошибок.
Проделаем несложный корреляционный анализ. Есть 2 массива значений температуры для дней N и N+1,
например, для дня новолуния и дня следующего за ним. Если в день N происходит перелом хода температур, то коэффициент
корреляции (далее K) будет близок к нулю. Коэффициент корреляции
описывает «похожесть» двух рядов друг на друга. Для нашего исследования для всех пар рядов N и N+1
K больше 0.95, кроме пары «новолуние – день +1» и «день +1 – день
+2», когда он падает до 0.93.
Есть еще один метод анализа, применимый здесь. Посчитаем, сколько раз
из 210 рядов температура повышалась или понижалась. Для этого образуем новую
матрицу из разницы температуры между днем
N
и N-1. При случайном ходе
температур ожидаемое количество понижений и повышений должно быть равным 105.
Для исследуемого набора данных график приведен на рис.2
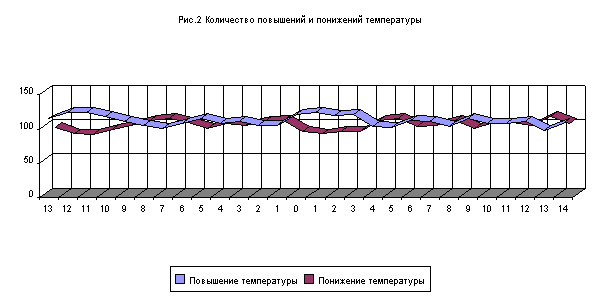
Понятно большое число повышений (ряд 1) возле полнолуния, этому
соответствует повышение температуры от полнолуния на рис. 1. Этому же
соответствует и большое (124) число повышений возле новолуния. Погрешность,
рассчитываемая для равномерно распределенных величин, для нашего случая будет
12.32. Т.е. найденные нами закономерности все-таки неслучайны. Причем,
превышение потеплений над похолоданиями держится от нулевого до +4 дня. После
этого (секстиль Солнце – Луна) число повышений равно числу понижений
температуры. Связывая это с графиком
на рис.1 можно сделать вывод о гораздо более глубоких похолоданиях, чем
потеплениях от растущего секстиля Луны к полнолунию.
Весьма интересно будет провести анализ по нахождению новолуний в
стихиях и крестах Зодиака (рис.3, рис.4)
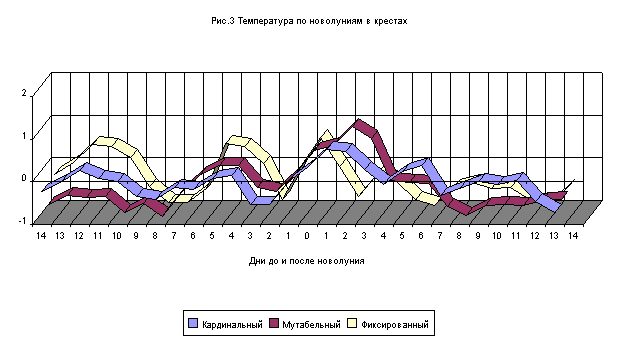
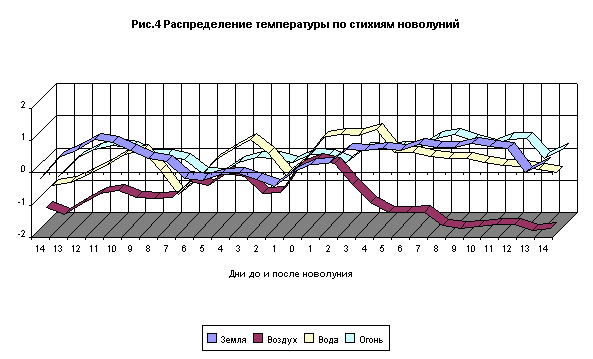
В то время, как в распределении по крестам мы не находим большой
разницы, распределение по стихиям дает пищу для размышлений. Например, ярко
выраженный ход температуры при новолуниях в знаках воздуха. Явное падение
температуры после новолуния. При новолуниях в знаках воды можно ожидать
потеплений вблизи убывающего секстиля и после новолуния. Теплым оказывается
месяц и при новолуниях в знаках земли, но с убыванием температуры к новолунию.
Вот вам и новый метод прогнозирования – смотрим, ГДЕ БУДЕТ, а не ГДЕ БЫЛО
полнолуние. Парадокс! Однако именно это объясняет, почему январь с полнолунием в Козероге теплее,
чем самый холодный месяц года - февраль с полнолунием в Водолее. Так, в этом
году в январе полнолуние с Солнцем в середине Козерога, и в феврале –
полнолуние с Солнцем в середине Водолея. Можно ожидать относительно теплого
января и очень холодного начала февраля, (полнолуние). Это вполне может
оправдывать смещение волн холода в пределах нескольких недель в ту или иную
сторону.
1.2 Осадки
Примерно таким же образом анализировались осадки. Данные не
нормировались по рядам, т.к. в осадках нет сезонного хода. Подсчитывалось
среднее количество осадков (рис.5), число дней с осадками (рис.6) для каждого
дня.
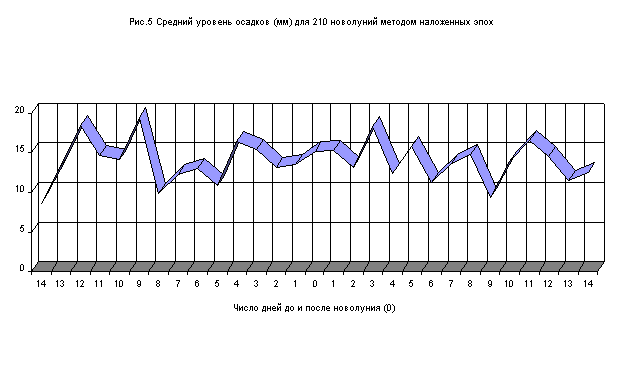
Как видно, наибольшее количество осадков приходится на убывающие трин и секстиль (10 и 4 дня до новолуния соответственно) и на 3 день после новолуния, а наименьшее – возле полнолуния, причем существенно, подтверждая тезис Грина о полной Луне, «разгоняющей облака» Во время новолуния не происходит никаких изменений.
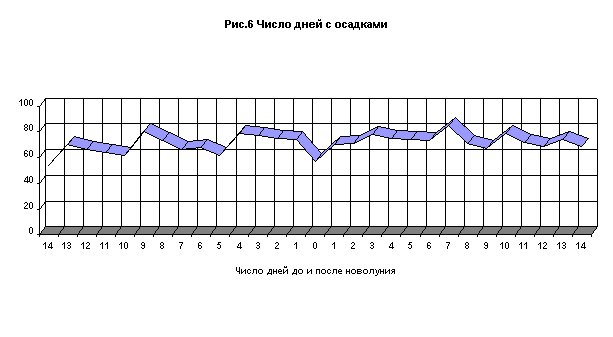
Из анализа рисунков 3 и 4 видно, что осадки после в полнолуние и после
него гораздо более интенсивны, чем
до него, т.к. численность дней с осадками после полнолуния меньше.
2. Выводы
Проведенный простой анализ
рядов температуры и осадков дает возможность сделать следующие выводы:
- Температура практически не зависит от
лунных фаз. Все
изменения находятся внутри зоны ошибок. Однако сразу после полнолуний и новолуний большое число повышений
температуры можно считать статистически обоснованным. Основываясь
на этом можно сделать вывод о правильности приведенных наблюдений Лявуа о
действии карты фаз Луны.
- Представляет прогностический интерес
поведение температурных рядов распределенных по стихиям знаков Зодиака.
- Выделяются
количеством осадков убывающие трин и секстиль Луны. Если температура действительно может
испытывать переломы на фазах Луны, то
осадки никак не связаны с
последними, кроме полнолуния, когда действительно мало дней с
осадками, но они более интенсивны.
Литература
[1] Sergey Tarassov, (Canada), Alphee Lavoie, (USA) Correlation between extraterrestrial factors and some terrestrial processes: Case Study/ The World Astrology Rev. #6, 2002/ http://trounev.com/thewar/No6/CaseStudy.htm
[2]
Предсказание
погоды с помощью астрометеорологии, Лондон
1912
[3] "Weather Predicting by Astro-Meteorology" by H.S.Green (перевод А.Колесников)
[4]
Бударовский А.И. Методологические проблемы астрологических прогнозов
погоды/ www.astrolcrimea.nm.ru
[5]
Лявуа „Потеряй эту книгу и найди ее с
помощью хорарной астрологии”, 1995
[6] П. Максимов, В. Стальнов. Астрология и погода.
Альманах НАА №1