Астрология и Астрофизика
Динамика Солнечной системы и глобальное
потепление
©Vladimir
Shashin (Санкт-Петербург)
В этой статье методом вейвлет-анализа
исследованы характерные циклы в климатических данных (температура и облачность)
за длительный период с 1901 по 2001 для разных стран – России, Англии, Канады,
США, Австралии, Швейцарии. Найденные циклы сравниваются с циклами обращения
планет Солнечной системы. Обнаружена корреляция климатических циклов с циклами
планет Солнечной системы.
Сделана статистическая оценка степени влиянии планет на климат и на ее
основе дан прогноз изменения климата планеты вплоть до 2100 года. Согласно нему
потепление прекратится к 2030-40 годам, затем в течение 40-80 годов температура
будет падать.
Введение
Локальным климатом называют совокупность
атмосферных условий за многолетний период, присущую данной местности в зависимости
от ее географической обстановки [1]. Основными климатообразующими процессами
являются теплооборот, влагооборот и атмосферная циркуляция. Глобальный климат
определяется уже не только географическими, но и астрономическими факторами.
Согласно [1], ими являются светимость Солнца, положение и движение Земли в
Солнечной системе, наклон оси вращения Земли и скорость ее вращения.
Смена эпох, ледниковые периоды и другие
циклы в природе связаны с циклическими
изменениями эксцентриситета орбиты Земли, ее оси вращения и прецессии.
Они известны как циклы Миланковича по имени сербского геофизика, открывшего их
в 20-е годы прошлого века (см. например http://www.cru.uea.ac.uk/cru/info/causecc/
).
Изменения солнечной радиации играют
основную роль в изменениях земного климата. Это преимущественно тепловая радиация
в диапазоне длин волн 0.1-4мкм.
47% приходящей от Солнца радиации - это видимый свет в интервале
0.4-0.76мкм. На инфракрасное излучение приходится 44%, а на ультрафиолетовое -
9% солнечной радиации. Земная поверхность и атмосфера также являются источниками
теплового излучения в диапазоне 4-100 мкм, причем интенсивность этого излучения
пропорциональна четвертой степени температуры. Как известно в составе
солнечного ветра, достигающего земной атмосферы, присутствуют потоки заряженных
частиц, в основном протонов и электронов, движущихся с большими скоростями.
Энергия этого излучения в 107 раз меньше энергии электромагнитной радиации
Солнца. Потоки частиц практически не проникает в атмосферу ниже уровня 90 км
над уровнем моря. Это излучение
зависит от солнечной активности или числа пятен на Солнце, которое еще
называют числами Вольфа. В них четко выделяется и будет проанализирован ниже
11-летний цикл.
Количественной мерой солнечной радиации
является энергетическая освещенность или плотность потока радиации - количество
радиации, падающей на единицу площади в единицу времени. Энергетическую
освещенность на верхней границе атмосферы на единицу площади, перпендикулярной
солнечным лучам, при среднем расстоянии Земли от Солнца называют солнечной постоянной
S0*. Смысл слова "постоянная" здесь в том, что эта величина
определяет радиацию, на которую еще не повлияла атмосфера. Согласно последним
наблюдениям солнечная постоянная равна 1367Вт/м2, причем ошибка измерения
составляет ±0.3%.
Энергетическая освещенность пропорциональна
квадрату расстояния между Землей и Солнцем. Она имеет наибольшее значение в
начале января и минимальное в начале июля, а в течение года изменяется на ±3.3%
из-за эллиптичности орбиты Земли. Последние измерения со спутников обнаружили, что за время порядка нескольких
дней и недель, она меняется на уровне нескольких десятых процента. Многолетние
измерения этого параметра отсутствуют. Ниже будет показано, что изменение плотности
потока солнечной радиации во времени коррелирует с циклами планет Солнечной
системы.
Около 30% падающей на Землю солнечной
радиации отражается назад в космическое пространство. Из остальных 70%, поступающих
в атмосферу часть поглощается различными газами, примесями, аэрозолями, водяным
паром и облаками, а часть рассеивается. На поглощение приходится 23% от общего
потока радиации и оно очень избирательно. Озон поглощает почти всю
ультрафиолетовую часть, это около 3% из этих 23%. Углекислый газ сильно
поглощает радиацию в инфракрасной области спектра, но его содержание в атмосфере
все же мало, поэтому его долей можно пренебречь [1]. Водяной пар является
основным поглотителем радиации, его доля в сумме с долей аэрозольного
поглощения около 15%, а оставшиеся 5% приходятся на облака. Поглощенная
радиация полностью идет на нагрев атмосферы.
Путем рассеяния солнечная радиация
ослабляется более значительно, чем при поглощении. Около 26% энергии общего
потока превращается в рассеянную радиацию и только около 2/3 затем достигает
земной поверхности, причем максимум этой энергии смещается в сторону синего
цвета, что объясняет голубой цвет неба.
На верхней границе атмосферы в среднем
выполняется условие радиационного баланса между приходящей и уходящей радиацией.
Оно глобальное, т.е. только по отношению к общему объему этих потоков тепла за
значительное время и различно для разных географических широт.
Изменения температуры в нижних слоях
атмосферы почти полностью определяются изменениями температуры земной поверхности
[1]. Земная поверхность участвует во многих процессах получения и передачи
тепла. К солнечной суммарной радиации добавляются теплообмен с атмосферой и
глубокими слоями почвы путем теплопроводности и получение/отдача тепла при испарении
и конденсации воды. Радиационный баланс на земной поверхности уравновешивается
нерадиационной передачей тепла [1].
Резкое увеличение в атмосфере парниковых
газов (углекислый газ, метан и др.) от промышленности, создает дополнительный
парниковый эффект, заключающийся в дополнительном увеличении радиационного
нагрева атмосферы. Изменения климата, вызванные этой причиной, сначала носят
локальный характер, т.е. заметно повышается температура над городами с развитой
промышленностью. При анализе температурных данных было замечено, что глобальная
температура воздуха (рис. 18) в конце двадцатого века увеличилась на 0.6
градуса. Этот эффект получил название глобального потепления. Из-за того, что
его начало совпало с началом индустриальной эры, это потепление объясняется в
основном антропогенными причинами, т.е. дополнительным парниковым эффектом.
Для оценок возможных изменений климата
создаются сложнейшие модели, которые обещают повышение температуры к 2100 году
от 0.9 до 5 градусов. В этих моделях глобальное потепление объясняется деятельностью человека -
промышленными выбросами парниковых газов. Однако эти модели не дают
убедительной картины начала периода потепления климата. Например, в Алжире, в
котором почти нет промышленности, а потому и нет практически выбросов
парниковых газов, начало этого периода хоть немного должно быть сдвинуто по
времени, но такого сдвига нет. Изменение ежегодной температуры для этой страны
почти идеально повторяет аналогичные изменения для США и для всего Северного
полушария. Объяснить это можно большой инерционностью процессов теплообмена в
атмосфере. Для того, чтобы температура повысилась, необходимо время на прогрев
всего слоя атмосферы и верхнего слоя почвы Земли. Поэтому возможную
антропогенную причину глобального потепления следует искать за десять-тридцать
лет до видимого начала роста температуры, т.е. в начале 50-х годов, когда
парниковых газов антропогенного происхождения было сравнительно мало. Поэтому
существуют и другие причины потепления климата, например, астрономическими,
связанные с динамикой Солнечной системы. Ниже будет показано, что явление
глобального потепления может быть вызвано астрономическими факторами и имеет
вполне предсказуемый характер.
Для нахождения периодичности, как в
климате, так и в Солнечной системе, будет использоваться вейвлет-анализ,
основам которого посвящена первая часть работы. Последовательности глобальных
аномалий температуры в приземном слое, используемые далее в расчетах,
заимствованы из архивов Hadley Center - http://www.met-office.gov.uk/research/hadleycentre/obsdata/globaltemperature.html,
с сайта Climatic Research Unit - http://www.cru.uea.ac.uk/cru/data/temperature/, и с сайта NASA - http://www.giss.nasa.gov/.
Все данные получены путем обработки базы
данных HadCRUT2, содержащей данные по отдельным станциям. Поверхность Земли с
учетом океанов разбивается на участки размером 5*5 градусов широты и долготы,
по ним проводится усреднение, далее получаются данные для северного и южного
полушарий и после этого глобальные ряды.
Климатические данные по отдельным странам
взяты из архива Тима Митчелла - http://www.cru.uea.ac.uk/~timm/index.html
. Среднемесячные температуры для Англии за период с 1659 по 2001 года взяты из
архивов Hadley Center.
2. Вейвлет-анализ временных рядов
Классическим методом исследования сигналов
в частотной области является разложение в ряд Фурье, вейвлет-анализ является
его развитием, устраняющим несколько недостатков, присущих этому методу. Так же
как и для Фурье преобразования для вейвлет-преобразования предложены способы
реализации, позволяющие значительно ускорить время вычислений. Собственно
только благодаря этому данный раздел математики, на самом деле известный очень
давно, стал в последнее время очень популярным. Сейчас вейвлеты находят
применение в обработке сигналов, сжатии изображений и данных, например, лежат в
основе стандарта MPEG4.
Как известно, преобразование Фурье не
всегда подходит для анализа сигналов, характеристики которых зависят от
времени. Например, спектры сигнала, представляющего собой сумму двух синусоид и
сигнала, меняющегося из одной синусоиды в другую, будут одинаковы. Это свойство
называется неоднозначностью преобразования Фурье. Для того чтобы избавиться от
этого, необходимо применять различные виды оконных преобразований, в которых
сигнал изучается по частям. Для этих преобразований, в свою очередь, возникает
проблема выбора ширины окна, потому что от нее зависит разрешающая способность
в области частот. Сделав же оконную функцию зависимой от частоты, мы и
переходим от оконного преобразования к вейвлет-преобразованию. Оно не просто
режет сигнал на куски, а выделяет из него компоненты разных масштабов и каждый
компонент анализируется с той степенью детализации, которая соответствует его
масштабу. По математической сути преобразование Фурье - это корреляция между
волной и сигналом. Вейвлет-преобразование же - это корреляция между сигналом и
коротким всплеском (вейвлетом), локализованным и в частотной области, и во
времени.
Вейвлет-преобразованием функции f(t)
называется выражение:
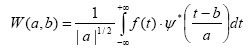 (1)
(1)
Входящая в это выражение функция называется базовым вейвлетом.
Звездочкой обозначена операция комплексного сопряжения. Параметр a называется
масштабом. Его аналогом является период Фурье преобразования. Большие значения
a соответствуют низким частотам, малые - высоким. Операция умножения на окно
как бы содержится в функции вейвлета. Вейвлетом может быть любая функция, но
как минимум первый статистический момент ее, т.е. среднее значение, должен быть
нулевым. Параметр b определяет временную
локализацию вейвлета и называется сдвигом. Он не имеет аналога в Фурье
преобразовании.
Существует множество различных функций
вейвлетов. В данной статье нас будет интересовать только вейвлет Морлета, позволяющий
хорошо обнаруживать периодические сигналы и впервые примененный для
исследования сейсмической активности. Это плоская волна, модулированная
гауссианой – рис. 1. Его функция имеет вид:
![]() (2)
(2)
Параметр альфа задает ширину гауссианы, k0
- ширину плоской волны. Обычно принимают
![]() и
и
![]() .
.
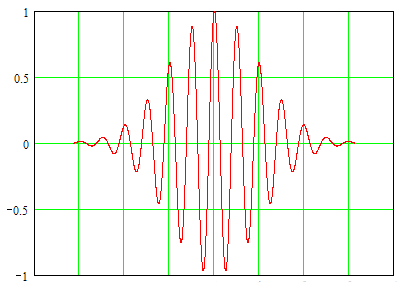
Рис. 1. Вейвлет Морлета
Вейвлет преобразование также можно
рассматривать как фильтрацию сигнала полосовым фильтром, ширина полосы пропускания
которого переменна.
По аналогии с преобразованием Фурье
вводятся понятие, соответствующее плотности энергии спектра:
![]() (3)
(3)
Из-за того, что в эту формулу входит
параметр b, ее называют локальным спектром энергии. Есть и глобальный спектр
энергии, который показывает распределение энергии по масштабам:
![]() (4)
(4)
При работе с ограниченными и дискретными
временными рядами эти формулы упрощаются.
Для оценки вейвлет преобразования
дискретной последовательности используются такие формулы:
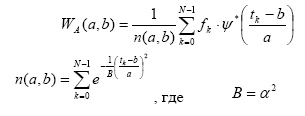 (5)
(5)
Функция WA называется амплитудной вейвлет
функцией, а ее локальный спектр энергии называется скалограммой:
![]() (6)
(6)
Оценка глобального спектра энергии
называется скейлограммой:
![]() (7)
(7)
Скейлограмма является аналогом сглаженной
периодограммы преобразования Фурье. Функция WA определяет корреляцию между
анализирующим вейвлетом, помещенным в точку b, с деталью временного ряда
размера, пропорционального масштабу a. Плотность энергии (6) определяется из
равенства Парсеваля и по ней путем простого интегрирования может быть построена
корреляционная функция между анализирующим вейвлетом и исследуемым временным
рядом. По определению она является статистической нормой некой
последовательности случайных величин. Это довольно важно, ведь при определенном
уровне абстракции, вспомнив про астрологию, именно с вейвлетами Морлета можно
отождествить все реальные события. Они, как правило, имеют волновой характер,
сначала причины, т.е. область роста, кульминацию и последствия - затухание. В
таком случае скалограмма (плотность энергии) может нами восприниматься как
функция распределения таких вейвлетов/событий/всплесков.
Они выводятся в виде трехмерных графиков,
где по осями x и y откладываются параметры a и b, а по оси z значение функции S(a,b). При этом по
оси масштабов (a) часто выбирается логарифмический масштаб, учитывающий
уширение спектра с увеличением масштаба.
Периодические сигналы на скалограмме
выглядят в виде максимумов, параллельных оси времени b.
Влияние дискретизации на характеристики
вейвлет-преобразования изучено и главный вывод состоит в том, что уменьшение
числа отчетов приводит к искажениям в высокочастотной области, т.е. на
небольших масштабах, оставляя низкочастотную область почти неизменной, понижая
лишь степень ее детализации. Контур скалограммы при увеличении числа отчетов
как бы все более ясно "проявляется из тумана" (например, как на рис.
39).
Перед вейвлет-анализом из исследуемой
последовательности необходимо удалить линейный тренд. Это постоянная составляющая
сигнала и низкочастотные колебания с периодами большими половины
рассматриваемого интервала. На скалограммах они выглядят как максимумы и
искажения вдоль границ и только мешают поиску периодичности. Для вычисления
линейного тренда будем использовать сглаживание последовательности с большим
числом точек.
Бывает так, что контуры линий на скалограммах
не позволяют проследить эволюцию частот во времени. Для этого выделяют максимумы
и строят скелетон скалограммы (8).
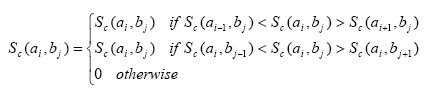 (8)
(8)
На трехмерных графиках скелетона
периодические составляющие вытягиваются вдоль оси времени, а шумовые перпендикулярно
ей. Этот график позволяет увидеть шумовые и периодические составляющие
раздельно. Для скелетона также можно строить его скейлограмму.
Если два сигнала имеют схожий характер
скалограмм или областей скалограмм или сходную периодичность при одинаковом
числе отсчетов и параметров анализирующего вейвлета, то это означает наличие
корреляции между этими двумя исследуемыми процессами.
3. Динамика Солнечной системы
Движение материальной точки P относительно
некоторого тела O, считающегося неподвижным, согласно теоретической механике, можно описать перемещением
радиус-вектора с началом в точке O и концом в точке P:
![]() (9)
(9)
Считая каждое небесное тело материальной
точкой, их движение относительно Земли можно описать такими вектор-функциями.
Значения их не могут быть любыми, а определяются законами гравитации, которые
являются связями данной системы.
Для расчетов положений планет в данной
работе используются швейцарские таблицы эфемерид (http://astro.com),
записанные в прямоугольной геоцентрической системе координат.
Радиус-векторы для каждого момента времени
можно сложить, получив траекторию движения некой точки, в которой есть информация
о движении каждой из планет:
 (10)
(10)
Если вывести на график нормализованный
модуль (длину) суммарного радиус-вектора L, то можно получить наглядное представление
об общем движении тел Солнечной системы.
Другим возможным вариантом такого
представления являются циклические индексы Барбо и Гано, основанные на сложении
угловых расстояний между планетами. Индекс Барбо - это среднее арифметическое
между угловыми расстояниями планет, взятыми попарно. Индекс Гано производный от
него, определяющий в какой фазе, сближения или удаления, находится каждая пара
планет. Отметим, что индексы Барбо и Гано широко используются в астрологических
исследованиях. При нахождении суммарного радиус-вектора учитываются и угловые
расстояния между планетами, поэтому имеется корреляция модуля вектора L и индекса Барбо – рис. 2. Коэффициент корреляции составляет
-0.81 (минус означает зеркальность).
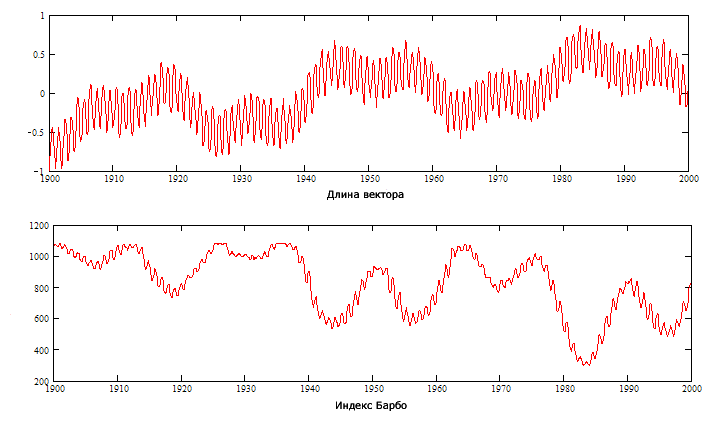
Рис. 2 Модуль радиус-вектора и индекс
Барбо для 20-го века
Модуль вектора L обладает интересным свойством. Если
использовать гелеоцентрическую систему координат и радиус-векторы строить от Солнца, то график модуля суммарного
радиус-вектора окажется точно таким же, как в геоцентрической системе.
Скалограмма и скейлограмма функции модуля
радиус-вектора для 20-го века представлены на рис. 3. Число точек - 4000. Каждый из максимумов соответствует
одной планете, дальние планеты за Сатурном оказались ненайденными, потому что
их периоды больше половины рассматриваемого интервала (100 лет). Отметим, что
при этом способе анализа не выявляется цикл Меркурия, а цикл Венеры (0.65 лет)
заметен только при очень большом увеличении. Тем не менее, метод является довольно точным в сравнении с
преобразованием Фурье, поскольку на периодограмме преобразования Фурье для
данного сигнала, грубо выделяются лишь основные периоды, но какую-то
дополнительную информацию из нее извлечь затруднительно. Кроме того, на периодограмме преобразования Фурье нет
четко выделенного цикла Луны,
период которого находится практически на пределе критерия Найквиста,
т.е. сравним с удвоенной частотой дискретизации.
По скэйлограмме рис.3, определив значения
максимумов по оси Z, можно вычислить относительные плотности энергии для планет,
но понять смысл этих чисел сначала непросто. Если не рассматривать годовой
цикл, то получится последовательность 1(Марс):6(Юпитер):18(Сатурн) четко
соответствующая отношениям межпланетных расстояний, а максимумы хорошо ложатся
на экспоненту (если повернуть оси). Это особенно четко видно на скалограмме для
прошлого тысячелетия (рис. 5, пунктир на скейлограмме). Становится понятным,
почему плохо проявлены циклы Венеры и Меркурия - просто их расстояния до Солнца
очень малы по сравнению с другими участниками небесного движения, а, значит, и
их плотности энергии на графике невелики и незаметны. К сожалению, период
Сатурна сильно отличается от стандартного (29.54 года). Это связано с тем, что
в рассматриваемый интервал помещаются всего три его цикла, максимум находится
на краю графика, где цена деления большая (она тоже растет логарифмически) и
имеет место интерференция сигналов. Нельзя забывать, что изучается
комбинированный сигнал. Поэтому на других скалограммах, например, при изучении
температур, можно ожидать примерно такого же смещения его максимума в область
больших масштабов.
Все это подтверждает хорошую точность
вейвлет-анализа и демонстрирует, как можно определять наличие или отсутствие в
различных последовательностях периодических составляющих и позволяет сравнивать
их.
Интересные результаты, получаются при
проведении вейвлет-анализа среза годового максимума, т.е. линии вдоль оси
времени на масштабе, соответствующем одному году. Но предварительно нужно
увеличить число точек по оси времени минимум до 400-600, чтобы число точек
сигнала для второго вейвлет-преобразования было достаточно большим.
Исследуемый сигнал, представленный на рис.
4, имеет слабые колебания амплитуды порядка 0.5% от постоянного уровня. Это
могут быть колебания орбиты Земли вокруг Солнца, заложенные в виде
коэффициентов в швейцарские эфемериды и усиленные интерференцией с составляющими
сигнала от других планет. На скалограмме этого сигнала - рис. 6, хорошо
выделяются периоды, соответствующие Юпитеру и Сатурну.
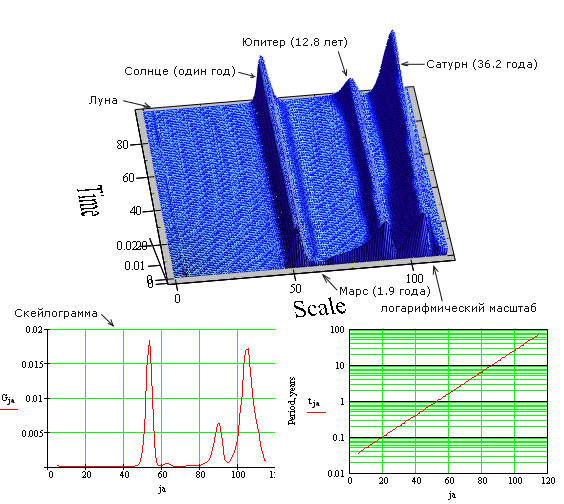
Рис. 3. Вейвлет-анализ модуля
радиус-вектора для 20-го века
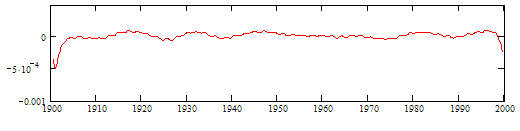
Рис. 4. Срез годового цикла
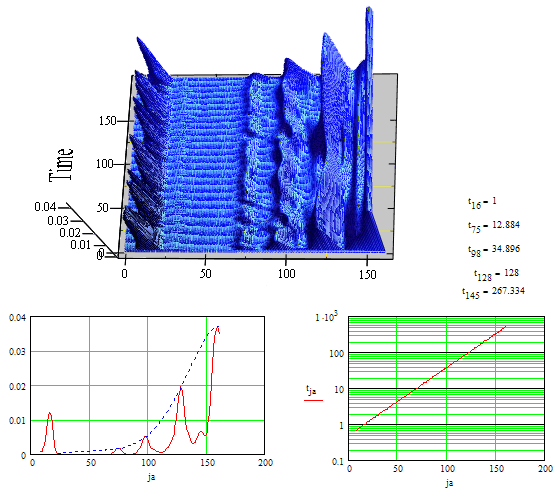
Рис. 5. Скалограмма последнего тысячелетия
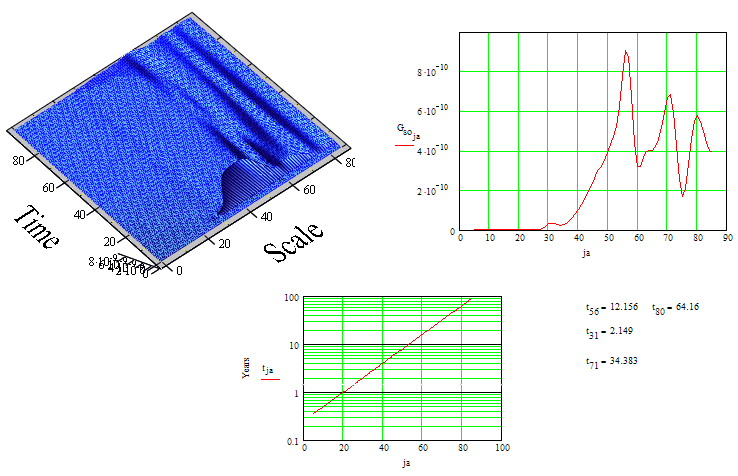
Рис. 6. Вейвлет-анализ годового цикла
Эти методы были применены для нахождения
циклов в климатических данных и циклы, с масштабами, соответствующими планетарным,
найдены в годовых срезах среднемесячных температур.
Довольно случайно на основе (10) была
получена функция, хорошо коррелированная с глобальными аномалиями температуры
(свою роль сыграли эксперименты с индексами Барбо). Возможно, что это можно
сделать не одним способом и возможно, что способ, изложенный ниже, далеко не
лучший, а сама корреляция справедлива только в некоторых уникальных случаях.
Тем не менее, этот факт позволяет составить прогноз дальнейшего глобального
потепления. Вычислим вектор, равный разнице между радиус-векторами из (10) для
начала и конца рассматриваемого интервала времени и поделим его пополам:
![]() (11)
(11)
Затем каждый радиус-вектор сложим с ним и
найдем нормализованный модуль:
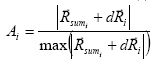 (12)
(12)
Полученная таким способом
последовательность A оказывается коррелированной с последовательностями
глобальных аномалий температур (не сглаженными) с коэффициентом 0.7, что показывает
линейную взаимосвязанность двух процессов - см., например, рис. 19. Учет границ
интервалов в (12) позволяет увидеть характерные именно для рассматриваемого
участка времени особенности небесной динамики, поскольку в этом случае дальние
планеты, такие как Плутон, периоды которых намного больше рассматриваемого
интервала, практически не влияют на внешний вид графика. Циклы в (12) идентичны
(10), постоянное смещение не оказывает влияние на периоды, но резко
увеличивается линейный тренд, энергия спектра как бы перетекает в него. Внешний
вид кривой L(t) при этом меняется существенно и является различным на разных
интервалах.
Продолжение в следующем
номере
Литература
1. Хромов С.П. Петросянц М.А.
"Метеорология и климатология", изд. МГУ им. Ломоносова, серия
"Классический университетский учебник", 2004.
2. Витязев В.В. "Вейвлет-анализ
временных рядов", изд. СПбГУ, 2001
3. Межправительственная группа экспертов
по изменению климата "Изменение климата 2001г.: научные аспекты ",
ЮНЕП, ВМО, 2001