Астрология и АстрофизикаГравитационные волны и структура спиральных галактикAlexander Trounev (Toronto, Canada)Гравитационные волны были впервые предсказаны на основе общей теории относительности [1]. Согласно этой теории гравитационные волны имеют столь малую амплитуду, что не могут быть обнаружены современными приборами. Интересно отметить в этой связи, что гравитационные волны действительно до сих пор не зарегистрированы, хотя предпринимались многочисленные попытки для их обнаружения. Возможно, что они и не будут обнаружены, поскольку согласно существующим представлениям связаны с искривлением метрики пространства. В модели [2] есть другой механизм возникновения гравитационных волн, связанный с изменением скорости света при флуктуациях плотности эфира, которые могут возникать, например, при вращении массивного центра гравитации. Рассмотрим модель этого явления. Исходная система уравнений имеет вид [2]:
Флуктуации плотности флюида приводят к флуктуациям квадрата скорости света по формуле:
Уравнение (2) описывает гравитационные волны, связанные с изменением плотности эфира, которые могут возникать, например, в звездах или в галактиках. Это уравнение нелинейное, но его можно линеаризовать вблизи мощного источника статической гравитации, потенциал которого описывается уравнением:
Подставляя это выражение в уравнение (2) и используя определение субстанционального времени, получим:
Поскольку уравнение (4) линейное, в нем следует учесть нестационарные эффекты, связанные с изменением потенциала при изменении мирового времени ("электромагнитные" волны). Тогда окончательно имеем:
Учитывая сферическую симметрию задачи, будем искать решения уравнения (5) в виде:
Здесь
Подставляя функцию (6) в уравнение (5) и разделяя переменные, находим уравнение для радиальной функции:
Заметим, что уравнение (8) совпадает по форме с уравнением для радиальной функции в задаче об атоме водорода в квантовой механике. Как известно, это уравнение имеет финитные решения при условии:
Отсюда находим собственные значения параметра затухания гравитационных волн (или их частоты):
Дадим интерпретацию полученным решениям. Мы предполагаем, что вращение тела описывается мировым временем, потому угол поворота зависит от угловой скорости и времени как
Реально можно наблюдать только угол поворота тела, поэтому выражая время через угол поворота, имеем
Сравнивая выражения (6) и (7), находим, что потенциал затухает при изменении угла поворота по закону
Рапеределение гравитационного потенциала или плотности флюида в пространстве по радиальной координате аналогично распеределению плотности волновой функции электрона в атоме водорода. Для основной моды при
Такой закон затухания потенциала позволяет объяснить формирование руковов спиральных галактик. Действительно, в фиксированный ммомент времени потенциал (или плотность наблюдаемой материи, которая пропорциональна гравитационному потенциалу, согласно второму уравнению (1)) является постоянным на линии спирали Архимеда
Интересно, что шаг спирали зависит только от угловой скорости вращения ядра. Размер же такой галактики зависит только от скорости света и периода обращения центра:
Однако структура такого типа галактик трудно наблюдаема, поскольку внешнему наблюдателю они могут казаться просто шаровым скоплением. Чтобы получить типичный случай плоской галактики закрученной в виде логарифмической спирали, предположим, что в выражении (6)
При больших значениях l амплитуда функции (11) имеет пик вблизи плоскости экватора и остается постоянной на линии
При малых значениях радиальной координаты уравнение (12) сводится к уравнению логарифмической спирали, а при больших значениях получаем спираль Архимеда. При этом логарифмическая спираль закручена в правую сторону, а Архимедова спираль - в левую. Число рукавов галактики зависит от степени синхронизации вращения ее центральной части и осцилляций плотности. Если частота осцилляций кратна частоте вращения,
Рис. 1. Модель однорукавной спиральной галактики (слева), построенная на основе (11) при l=7. Хорошо видно, как формируется рукав. На фото справа - однорукавная спиральная галактика NGC 4725 в созвездии Волос Вероники (Robert Nemiroff (MTU) & Jerry Bonnell (USRA))Таким образом, в рамках модели [2] показано, что стоячие гравитационные волны, обусловленные вращением центрального ядра галактики, являются причиной образования закрученных рукавов. В следующей статье мы рассмотрим гравитационные волны, которые могут быть обнаружены в пределах Солнечной системы. Ссылки 1. Albert Einstein. Relativity. The Special And The General Theory. !5-th Ed. NY, 1961. 2. Alexander Trounev. О фундаментальных свойствах информационной модели мира / The WAR, No 10 (46), October 30, 2005, http://trounev.net/thewar/No46/CR/CR.htm |
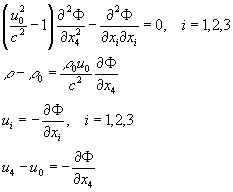 (1)
(1)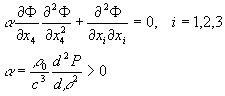 (2)
(2)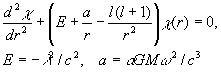 (8)
(8)