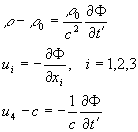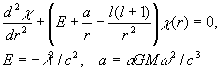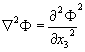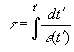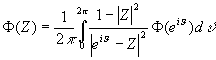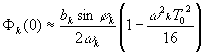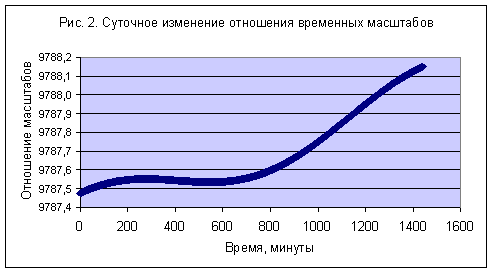
|
Chaos and Correlation История Земли в пяти измеренияхAlexander Trounev (Toronto, Canada)“Клише памяти” или, как называют его некоторые оккультисты, “Хроника Акаши”, является световым и звуковым отпечатком всех земных событий с момента рождения Земли на эфирном теле Вселенной – акаши. Лобсанг РАМПА В работах /1-2/ была рассмотрена модель течения эфирной субстанции в пространстве пяти измерений. Было установлено, что стационарные потоки эфира со скоростью света вблизи мощного центра гравитации обладают свойством вырождаться в четырехмерные вихревые течения, похожие по структуре на галактики или атомы водорода /2/. В настоящей работе дана интерпретация аналогичных течений вблизи поверхности земли. Показано, что эти течения приводят к возникновению своеобразных двумерных лакун в плоскости мирового (галактического) и локального (субстанционального) времени с отношением временных масштабов протекания процессов порядка 10 4. Наличие этих лакун позволяет объяснить некоторые эзотерические феномены, например исторические хроники, записанные на пластической субстанции (Хроники Акаши), феномен памяти о прошлых и будущих воплощениях, ясновидение и т.п. Лакуна времени вместе с атмосферой образует хроносферу, которая простирается в пяти измерениях. Образ любого исторического события, произошедшего в объеме хроносферы доступен наблюдателю в любой момент времени. Тем не менее, события в хроносфере упорядочены так, что кажутся далекими или близкими в геометрическом смысле. Этот порядок зависит от исторического времени события и образует историю Земли в пяти измерениях.1. Исходные уравнения и решения типа лакунРаспространение малых возмущений плотности эфира вблизи источника гравитации описывается уравнением /2/: (1) где Гравитационный потенциал вблизи поверхности земли представляется в виде суммы стационарного источника (потенциал нашей планеты) и нестационарных удаленных источников (Солнце, Луна, планеты Солнечной системы, поле Галактики): (2) Плотность и скорость потока эфира можно представить в форме: (3) Глобальные решения системы уравнений (1-3), описывающие течение эфира в атомах или галактиках, были изучены в работе /2/. Было показано, что в поле сферически симметричного стационарного источника решения можно представить в виде: (4) Здесь (5) Подставляя функцию (4) в уравнение (1) и разделяя переменные, находим уравнение для радиальной функции: (6) Заметим, что уравнение (6) совпадает по форме с уравнением для радиальной функции в задаче об атоме водорода в квантовой механике. Как известно, это уравнение имеет финитные решения при условии:
Отсюда находим собственные значения задачи: (7) Таким образом, глобальные решения уравнений (1-3) с одной стороны описывают структуру атома водорода, а с другой стороны структуру галактики /2/. В настоящей работе мы изучим локальные решения этих уравнений, зависящие только от времени и вертикальной координаты. Такое решение задачи возможно в тонком слое, прилегающем к поверхности земли и геометрически совпадающем с атмосферой. Рассмотрим решения уравнения (1) при условии, что гравитационный потенциал (2) не зависит от вертикальной координаты. В этом случае справедливо следующее выражение для оператора Лапласа: (8) где x3 - вертикальная координата. Подставляя выражения (2, 8) в уравнение (1), находим(9) Далее без ограничения общности положим (10) Полученное уравнение (10) описывает линейные колебания плотности эфира в узком слое, совпадающем с атмосферой. Решения уравнения (10) вида (11) при условиях Главная особенность решений типа лакун (11) заключается в том, что любое локальное возмущение, вызванное событием конечной длительности во времени dt', мгновенно доступно во всей плоскости . При этом масштабы длительности события связаны соотношением  . Это отношение масштабов является фундаментальной характеристикой лакуны. В приземном слое величина  слабо изменяется за один год - рис. 1 (данные для широты Москвы), и еще слабее за одни сутки - рис. 2 (данные на 3 июня 2005 года, время отсчитывается от полночи). По порядку величины масштаб галактического времени в десять тысяч раз больше, чем масштаб субстанционального времени. В среднем одна секунда субстанционального времени эквивалентна 2 часам 42 минутам галактического времени, одни сутки эквивалентны 26 годам 226 дням и 20 часам, а один год - 9723,133625 годам галактического времени. Субстанциональное время характеризует местные условия. С физической точки зрения это релятивистский эффект, имеющий порядок отношения орбитальной скорости планеты к скорости света. Именно этот эффект определяет интенсивность взаимодействия, как следует из уравнения (6). Галактическое время характеризует состояние Вселенной. Если земная реальность протекает в масштабе субстанционального времени, то при переключении сознания на поток галактического времени, все в мире замирает, поскольку кажущаяся скорость уменьшается почти в десять тысяч раз. С психологической точки зрения это означает возможность погружения в иной мир со своим порядком событий и своими законами существования.
Смысл решений типа лакун заключается в следующем. Предположим, что у нас имеется хронология исторических событий, упорядоченных в соответствии с календарем вдоль оси субстанционального времени t'. Каждое событие можно характеризовать длительностью и интенсивностью возмущения плотности эфира. В плоскостисобытию соответствует некоторая замкнутая область. Предположим, что это единичный круг с центром в начале координат. Используя функцию Жуковского,
можно отобразить внутренность круга на всю плоскость с разрезом от -1 до +1 вдоль оси субстанционального времени. Это будет образ события, как оно видится в истории в любой момент времени. Таким образом, решения типа лакун обеспечивают сохранение исторической информации на любом отрезке времени, пока существует хроносфера. Само событие, каким бы оно ни было, полностью определяется путем задания функции 2. Малые возмущения лакун, вызванные движением небесных телВ общем случае, когда
Тогда, с учетом слабой зависимости решений типа лакун от вертикальной координаты, оно приводится к виду: (12) Общее решение уравнения (12) можно представить в виде суммы решений типа лакун и частного решения неоднородного уравнения: (13)
Далее заметим, что в пределах хроносферы параметр
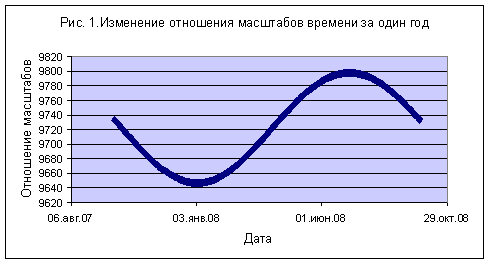
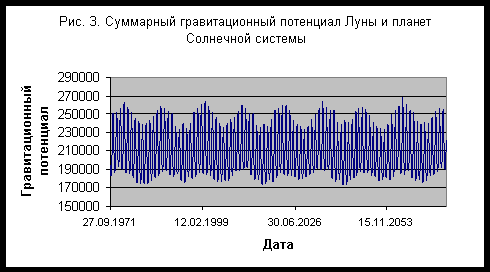
Действительно, основной вклад в гравитационный потенциал вблизи земли вносит Солнце. Из-за малой эллиптичности земной орбиты гравитационный потенциал Солнца испытывает слабые сезонные колебания, с амплитудой около 0,0167 от средней (статической) величины, составляющей 8,87 826*108 м2/сек2 . Вторым по величине является собственное гравитационное поле Земли, которое также меняется очень слабо. Планеты периодически сближаются и удаляются из-за движения Земли и собственного движения, поэтому их суммарный потенциал колеблется около среднего значения - рис. 3, которое составляет 210631,0031 м2/сек2 (вычислено за период 100 лет, начиная с 27 сентября 1971 г.). На рис. 3 отчетливо просматриваются колебания потенциала, вызванные обращением Юпитера, который и дает основной вклад в суммарный гравитационный потенциал планет. Если из суммарного гравитационного потенциала вычесть потенциал Луны, тогда среднее значение составит 197876,2649 м2/сек2, т.е. потенциал Луны на порядок меньше, чем суммарный потенциал планет.
Амплитуда колебаний гравитационного потенциала Солнца составляет 1,482669*10 7 м2/сек2, вклад планет в 100 раз меньше, а вклад Луны в 1000 раз меньше (отметим, что для приливного воздействия соотношения будут иные). Это обстоятельство позволяет построить теорию возмущений для уравнения (13). Таким образом, в первом приближение имеем:(14) Наиболее простое решение типа лакун, согласованное с интуитивным представлением о линейном времени, имеет вид:
Нормировка выбрана так, чтобы в случае статической гравитации получалось фоновое гравитационное поле. Подставляя это решение в уравнение (14), находим (15) Переменную часть гравитационного поля в общем случае можно представить в виде суммы гармоник, соответствующих периодам обращения Земли и планет: (16) Частное решение уравнения (15) с правой частью в форме (16) имеет вид: (17) Используя это решение можно оценить вклад отдельных гармоник как Рассмотрим задачу о нахождении аналитической функции в единичном круге по заданному значению на его границе в форме (17). Как известно, решение этой задачи дается интегралом Пуассона: (18) Используя это выражение можно вычислить значение функции в центре круга для отдельной гармоники. Положим (19) где T0 - характерная длительность события в масштабе субстанционального (земного) времени.Полученному выражению можно придать наглядную форму при условии (20) Заметим, что физический смысл имеет производная по времени от потенциала, вычисляя которую, получим (21) Следовательно, любое событие, если только оно ограниченно во времени, вызывает изменение плотности эфира (и гравитационного потенциала), в соответствии с (21). В качестве примера события назовем существование в физическом теле, которое имеет начало (рождение) и конец (смерть), тогда T0 - это продолжительность жизни. В процессе жизни происходит вытеснение эфира из некоторого объема лакуны, пропорционально продолжительности жизни. Тем самым создается влияние на весь объем лакуны. Это влияние похоже на влияние воздушного пузыря в жидкости. Оно не существует само по себе, но возникает лишь как реакция на изменение гравитационного потенциала, вызванного движением планет. В рамках этой простой модели можно объяснить суть фундаментальной зависимости судьбы человека и других живых существ от положения планет. Жизнь использует вариации плотности эфира, вызванные движением планет, для противостояния гравитации, создавая себе зону существования в плоскости времени.Поскольку мы имеем дело с эллиптическим уравнением на плоскости, его фундаментальное решение типа источника имеет вид
Следовательно, возмущение плотности является анизотропным в плоскости (22) Экстремумы функции (22) лежат на линиях  суток, т.е. нормальный сон должен длиться примерно 8 часов 40 минут, что довольно точно соответствует медицинской норме. С другой стороны, длительность жизни также соответствует смене знака самой низкочастотной гармоники, например, Нептуна, имеющего период обращения 164,491 лет. Тогда люди должны жить в среднем 104,77 года. Такое влияние Нептуна видимо соответствует жизни под наблюдением врачей и смерти в госпитале, либо жизни в медитациях и таинственному уходу в нирвану.
В заключение отметим, что мы рассматриваем хроносферу как бесконечную плоскость времени, хотя время существования планеты Земля также ограничено, как и время любого существа . Тем не менее, это время исчисляется миллиардами лет, что, по сути, равносильно бесконечной протяженности хроносферы. Всякое живое существо занимает в хроносфере конечную область изоморфную кругу на плоскости времени. Спрашивается, можно ли создать живое существо, способное заполнить собой всю хроносферу? Как не странно, но на этот вопрос можно ответить утвердительно. Машина жизни устроена так, что каждое новое поколение осваивает свой участок хроносферы. Это похоже на колонию бактерий, которые размножаются на поверхности питательной среды. Популяция это и есть живое существо, которое пытается освоить всю хроносферу. Отметим также, что окружность, ограничивающую событие жизни на плоскости времени, можно отобразить на окружность Зодиака, чем устанавливается однозначное соответствие между событиями жизни и элементами карты рождения.Наконец, тот факт, что состояние эфира в лакуне зависит главным образом от гравитационного потенциала, не исключает возможность влияния электромагнитного поля, чему будет посвящена следующая работа.
Ссылки
|
- параметр сжимаемости эфира; 
- плотность и давление эфира; 
- гравитационный потенциал; 
- скорость света; 
- локальное (субстанциональное) и мировое (галактическое) время соответственно. 
- сферические функции, которые выражаются через присоединенные функции Лежандра
. Учитывая, что гравитационный потенциал является всегда отрицательным и, полагая 
, представим (9) в форме:
, будем назвать решениями типа лакун. Отметим, что в пределах толщины атмосферы отношение вертикальной координаты к скорости света является малой величиной порядка нескольких микросекунд. Поэтому с большой степенью точности далее положим 
на границе круга (задача Дирихле). Вообще говоря, исторические события не могут вызвать сколь ни будь заметное изменение плотности эфира, если только сами они не вызваны природными катаклизмами. Поэтому функция 
, можно построить теорию возмущений для учета влияния движения небесных тел на образы событий в лакунах. Для этого в уравнении (10) сделаем замену переменных:
, 
. 
, 
. Из этого соотношения следует, что при сопоставлении гармоник, вклады Солнца и Юпитера различаются уже только в 10 раз, поскольку период обращения Юпитера составляет 11,86 лет. 
. В этом случае, раскладывая подынтегральное выражение в правой части (20) в ряд Тейлора, находим приближенное выражение 
, т.е. область влияния события жизни в масштабе галактического времени примерно в десять тысяч раз больше, чем время жизни. Это и есть главная причина колоссальной возможности проникновения сознания в толщу времени. Интересное следствие можно вывести из уравнения (20). В пределах земли минимальным периодам являются сутки. Если бодрствование