Aerodynamics
The friction parameter of the turbulent boundary layer over
the rough surface with 2D and 3D roughness elements.
Turbulent
boundary layer in pressure gradient.
Turbulent boundary layer
over rough surfaces with 3D and 2D roughness elements
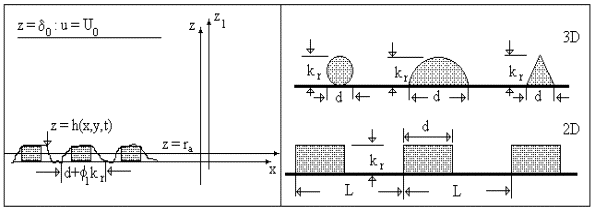
Figure
1. The scheme of the turbulent flow over a rough surface (left), and the
roughness elements geometry: spheres, spherical segments, conical elements (3D)
and transverse rectangular roods (2D).
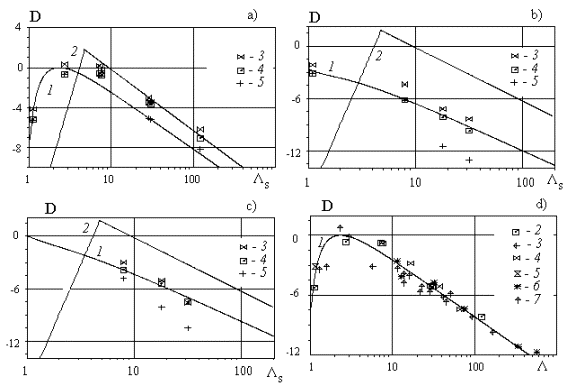
Figure 2. Roughness density effect on the turbulent flow in a case of 3D
roughness elements: a) spheres; b) spherical segments; c) cones; d) the
generalised correlation.
The mean velocity profile is given by 
. The roughness density parameter proposed by Dvorak (1969)
is given by 
, where S is the total roughness area, 
is the whole
area. The universal roughness density parameter for 3D roughness elements
depends on the Dvorak's roughness density parameter 
, where a is the geometrical parameter
defined as coefficient in the equation for the averaged roughness element
height 
, b0
is the friction parameter of
the roughness elements.
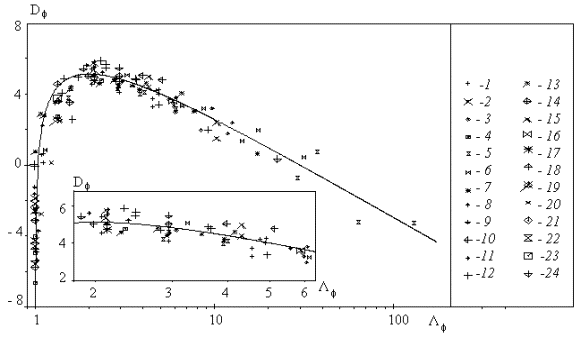
Figure 3. Roughness density effect on the turbulent flow in a case of 2D roughness
elements: the experimental data of various authors are shown with symbols 1-24.
The universal roughness density parameter depends on the Dvorak's parameter as
follows 
, here f is
the re-circulation zones parameter: 
.
The mean velocity profile
parameter is given by 
where b1 =0.12.
To read more
about the turbulent flows over rough surfaces please copy Chapter3.zip file
556K with MS Word97 doc Model
of turbulent flows over rough surfaces by A P Trunev .
Turbulent boundary layer
flow in pressure gradient
The
constructive model of turbulence has been developed for the case of
turbulent boundary layer flow in pressure gradient as follows:
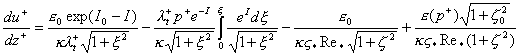
where 
is the dynamic
Reynolds number.
This model is based on three
assumptions:
1)
the
turbulent mixing parameter c depends on the transition layer scale lt;
2)
the
mean velocity profile in the inner layer depends on the transition layer scales
and on the dimensionless pressure gradient 
;
3)
the mean
velocity profile in the outer region depends on the outer layer variable 
, where y0 is the middle position of the
mixing layer, z* is the mixing layer parameter.
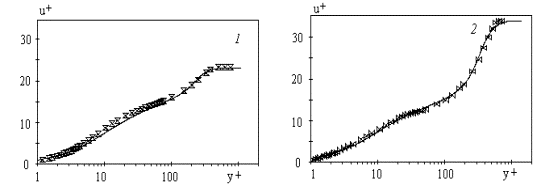
Figure 4. The estimated mean velocity profiles in the turbulent boundary
layer in adverse pressure gradients for p+=0.00898; 0.0251 - the solid lines
1-2 accordingly, and the experimental data (symbols) by Nagano et al (1992).
The function of pressure gradient
parameter estimated from the experimental data by Nagano et al (1992) for the turbulent boundary layer in adverse pressure
gradients at low Reynolds number as follows
.
The mixing layer parameters also
have been established from the experimental data and they shown to be z* =0.27, y0=H/2.
The computed mean velocity profiles
together with the experimental data by Nagano et al (1992) are shown in Figure 4.
To read more about the constructive theory of turbulence copy ZIP file (261K) with MS Word2000 doc: "Theory and constants of wall turbulence" by A P Trunev.
References
Trunev A. P. Theory of Turbulence and Turbulent Transport in the Atmosphere. WIT
Press, 2001.
Trunev A. P. Theory
of Turbulence, Russian Academy of Sciences, Sochi, 1999.
Dvorak , F. A. Calculation of Turbulent Boundary Layer on Rough Surface in Pressure Gradient. AIAA Journal 7, 9, 1969.
Nagano, Y., Kasagi, N., Ota, T., Fujita, H., Yoshida, H. & Kumada,
M. 1992 Data-Base on Turbulent Heat
Transfer, Department
of Mechanical Engineering, Nagoya Institute of Technology, Nagoya, DATA No. FW BL004.