Home

Fluid Mechanics

Thermal boundary layer

The constructive model of turbulence was developed to estimate the turbulent transport of heat in the boundary layer. This model is based on two assumptions:

1)      the turbulent mixing parameter c depends on the transition layer scales;

2)      the mean temperature profile depends on the thermal sublayer scale  as well as on the transition layer scales (here Pr is the Prandtl number, kh  is the constant that approximately equals to the von Karman's constant).

 

With this assumptions the mean temperature gradient in a steady turbulent flow with the heat flux applied to the wall can be written in the form:

 

 

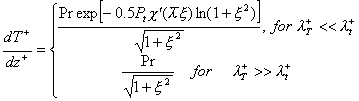
where , Tg is the wall temperature, T is the turbulent flow temperature,  is the scale of temperature, qH is the heat flux from the wall to the flow, cp is the specific heat at constant pressure of the gas,  is the parameter dependent on the Prandtl number. As it was established the parameter Pt(Pr) can be approximated in the range of the Prandtl number 2<Pr<1000 as follows: .

The boundary conditions on smooth wall and for the long distance from the wall are given by

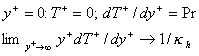
The estimated mean temperature profiles are shown in Figure 1 by solid lines together with the profiles computed on the model of Sebeci (1972) - they are shown by square symbols. The agreement between two models in general is good. The constant kh  and the temperature profiles also were calculated in the range 0.4<Pr<1.5 - see Figure 2.

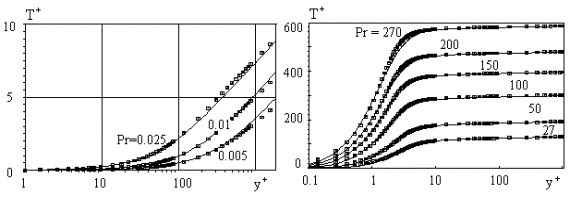
Figure 1. The estimated mean temperature profiles (solid lines) in the turbulent boundary layer at small Prandtl number (left) and at large Prandtl number (right). The square symbols -the model of Sebeci (1972).

 

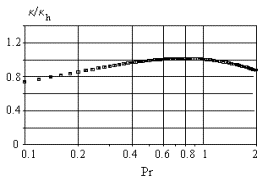
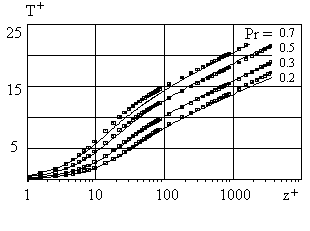
Figure 2. The ratio  versus the molecular Prandtl number and the estimated mean temperature profiles (solid lines).

 

Turbulent boundary layers in roughened tubes 

 

 

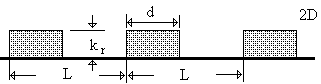
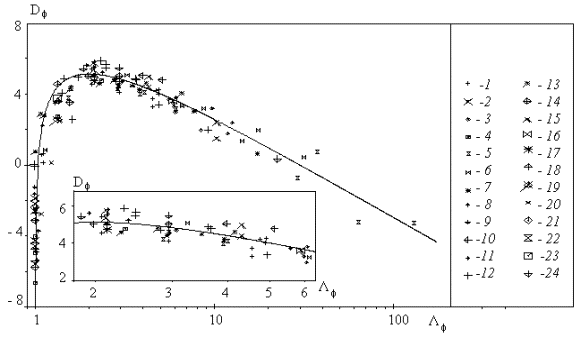
Figure 3. Roughness density effect on the turbulent flow in a case of 2D roughness elements: the experimental data of various authors listed in Table 1 are shown with symbols 1-24. The universal roughness density parameter depends on the Dvorak's parameter as follows , here f  is the re-circulation zones parameter:

.

The mean velocity profile is given by   where

 . Here b1 =0.12.

 

Table 1

Authors

Year

Geometry

Symbol

Möbius

1940

Tube

10.0-29.22

0.3-2.20

3

Chu & Streeter

1949

Tube

1.95-7.57

0.93

4

Sams

1952

Tube

2.0-2.3

0.88-1.37

9

Nunner

1956

Tube

16.36

0.8

16

Koch

1958

Tube

9.8-980

1.0-5.0

5

Fedynskii

1959

Annulus

6.67-16.7

1.0

10

Draycott & Lawther

1961

Annulus

2.0

1.0

2

Skupinski

1961

Annulus

Tube

2.0-41.0

22.2-133.4

1.0

2.0

6

Savage & Myers

1963

Tube

3.66-43.72

1.33-2.67

13

Perry & Joubert

1963

Wind tunnel

4.0

1.0

19

Sheriff, Gumley & France

1963

Annulus

2.0-10.0

1.0

14

Gargaud & Paumard

1964

Tube

Annulus

1.8-16.0

10.0-16.0

1.0-1.67

1.0

1

 

Bettermann

1966

Wind tunnel

2.65-4.18

1.0

20

Massey

1966

Annulus

7.53-30.15

1.06

15

Kjellström & Larson

1967

Annulus

2.02-38.52

0.086-4.08

12

Fuerstein & Rampf

1969

Annulus

2.91-25.04

0.42-2.50

8

Lawn & Hamlin

1969

Annulus

7.61

1.0

17

Watson

1970

Annulus

6.49-7.22

1.0

11

Stephens

1970

Annulus

7.20

1.0

18

Webb, Eckert & Goldstein

1971

Tube

9.70-77.63

0.97-3.88

7

Antonia & Luxton

1971

Wind tunnel

4.0

1.0

21

Antonia & Wood

1975

Wind tunnel

2.0

1.0

22

Dalle Donne & Meyer

1977

Annulus

4.08-61.5

0.25-2.0

24

Pineau, Nguyen, Dickinson & Belanger

1987

Wind tunnel

4.0

1.0

23

 

 

 

 To read more about the turbulent flows over rough surfaces please copy Chapter3.zip file 556K with MS Word97 doc Model of turbulent flows over rough surfaces by A P Trunev .  

The computed mean velocity profiles together with the experimental data by Nagano et al (1992) are shown in Figure 4.

To read more about the constructive theory of turbulence copy ZIP file (261K) with MS Word2000 doc: "Theory and constants of wall turbulence" by A P Trunev.

References

Trunev A. P. Theory of Turbulence, Russian Academy of Sciences, Sochi, 1999.

Cebeci T. 1973 A model for eddy conductivity and turbulent Prandtl number, J. Heat Transfer, 95, 227.

Antonia, R.A. & Luxton, R.E. 1971 The Response of a Turbulent Boundary Layer to a Step Change in Surface Roughness, Pt. 1. Smooth to Rough. J. Fluid Mech., 48, 721-762.    

Antonia, R.A. & Wood, D.H. 1975 Calculation of a Turbulent Boundary layer Downstream of a Step Change in Surface Roughness. Aeronautical Quarterly, 26, 3, 202-210.

Bettermann, D. 1966 Contribution a l’Etude de la Convection Force Turbulente le Long de Plaques Regueuses. Int. J. Heat and Mass Transfer, 9, 153.

Cantwell, B. J., Coles D. & Dimotakis, P. 1978  Structure and entrainment in the plane of symmetry of a turbulent spot, J.  Fluid Mech., 87, 641-672.

Cebeci, T. & Bradshaw, P. 1984 Physical and Computational Aspects of Convective Heat Transfer, Springer-Verlag, NY.

Chu, H. & Streeter, V.L. 1949 Fluid flow and heat transfer in artificially roughened pipes. Illinois Inst. of Tech. Proc. No. 4918.

Clauser, F. 1956 The Turbulent Boundary Layer. Advances in Applied Mechanics, vol. 4, pp.1-51. 

Coleman, H. W., Hodge, B. K. & Taylor, R. P.  1984 A Revaluation of Schlichting’s Surface Roughness Experiment. J. Fluid Eng. 106, 3.

Data-Base on Turbulent Heat Transfer/ Nagano Y., Kasagi N., Ota T., Fujita H., Yoshida H., Kumada M. Department of Mechanical Engineering, Nagoya Institute of Technology, Nagoya.  DATA No. FW BL004.

Dirling, R.B., Jr. 1973 A Method for Computing Roughwall Heat-Transfer Rate on Re-Entry Nose Tips. AIAA Paper, 73-763. 

Draycott, A. & Lawther, K.R. 1961 Improvement of fuel element heat transfer by use of roughened surface and the application to a 7-rod cluster. In Int. Dev. Heat Transfer, Part III, pp. 543-52, ASME, NY.

Donne, M. & Meyer, L. 1977 Turbulent Convective Heat Transfer from Rough Surfaces with Two-Dimensional Rectangular Ribs. Int. J. Heat Mass Transfer, Vol. 20, pp. 583-620. 

Driest, E.R. Van . 1956  On turbulent flow near a wall. J. Aero. Sci. 23, 1007.

Dvorak , F. A.  1969 Calculation of Turbulent Boundary Layer on Rough Surface in Pressure Gradient. AIAA Journal 7, 9.

Fedynskii, O. S. 1959 Intensification of heat transfer to water in annular channel. In Problemi Energetiki,  Energ. Inst. Akad. Nauk USSR (in Russian).

Fuerstein, G. & Rampf, G. 1969 Der Einfluß rechteckiger Rauhigkeiten auf den Wärmeübergang und den Druckabfall in turbulenter Ringspaltströmung. Wärme- und Stoffübertragung, 2 (1), 19-30.

Gargaud, I. & Paumard, G. 1964 Amelioration du transfer de chaleur par l'emploi de surfaces corruguees. CEA-R-2464.

Grabov, R.M. & White, C.O. 1975 Surface Roughness Effects on Nose Tip Ablation Characteristics, AIAA Journal, 13, pp. 605-609. 

Jackson, P.S. 1981 On the displacement height in the logarithmic wind profile.  J. Fluid Mech., 111, 15-25.

Kind, R. J. & Lawrysyn, M. A. 1992 Aerodynamic Characteristics of Hoar Frost Roughness. AIAA Journal 30, 7, 1703-7.

Kjellström, B. & Larsson, A. E. 1967 Improvement of reactor fuel element heat transfer by surface roughness. AE-271. Data repoted by Dalle Donne & Meyer (1977).

Klebanoff, P. S. 1954 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA Tech. Note, 3178.

Koch, R. 1958 Druckverlust und Wärmeübergang bei verwirbelter Strömung. ForschHft. Ver. Dt. Ing. 469, Series B, 24, 1-44.

Kuroda, A., Kasagi, N. & Hirata, M. 1989 A direct Numerical Simulation of the Fully Developed Turbulent Channel Flow. In International Symposium on Computational Fluid Dynamics, Nagoya, pp. 1174-1179.

Laufer, J. 1954 The structure of turbulence in fully developed pipe flow. NACA Tech. Note 2954.

Lawn, C. J. & Hamlin, M. J. 1969 Velocity measurements in roughened annuli. CEGB RD/B/N 2404, Berkley Nuclear Laboratories.

Massey, F.A. 1966 Heat transfer and flow in annuli having artificially roughened inner surfaces. Ph. D. Thesis, University of  Wisconsin.

Monin, A.S. & Yaglom, A.M. 1965 Statistical Fluid Mechanics: Mechanics of Turbulence. The MIT Press.

Möbius, H. 1940 Experimentelle Untersuchung des Widerstandes und der Gschwindig-keitsverteilung in Rohren mit regelmäßig angeordneten Rauhigkeiten bei turbulenter Strömung. Phys. Z. 41, 202-225.

Nagano, Y.& Tagawa, M. 1991 Turbulence model for triple velocity and scalar correlation. In Turbulent Shear Flows 7 (F. Durst, B. E. Launder, W. C. Reynolds, F. W., Schmidt, J. H. Whitelaw, eds), Springer, Berlin, Heidelberg, New York , pp. 47-62.

Nagano, Y., Tagawa M. & Tsuji. T. 1992 Effects of Adverse Pressure Gradients on Mean Flows and Turbulence Statistics in a Boundary Layer.  8th Symposium on Turbulent Shear Flows proceedings.

Nikuradse, J. 1933 Strömungsgesetze in Rauhen Rohren. ForschHft. Ver. Dt. Ing.  361.

Nunner, W. 1956 Wärmeübergang und Druckabfall in rauhen Rohren. ForschHft. Ver. Dt. Ing. 455.

Osaka, H. & Mochizuki, S. 1989 Mean Flow Properties of a d-type Rough Wall Boundary Layer in a Transitionally Rough and a Fully Rough Regime. Trans. JSME ser. B, Vol.55, No.511, 640-647.

Perry, A.E. & Joubert, P.N. 1963 Rough-Wall Boundary Layers in Adverse Pressure Gradients. J. Fluid Mech., 17, 2, 193-211.

Pineau, F., Nguyen, V. D., Dickinson, J. & Belanger, J. 1987 Study of a Flow Over a Rough Surface with Passive Boundary-Layer Manipulators an Direct Wall Drag Measurements. AIAA Paper, 87-0357.

Prandtl, L. 1933 Neuere Ergebnisse der Turbulenzforschung. VDI -Ztschr.  77, 5, 105.

Raupach, M.R. 1992 Drag and drag partition on rough surfaces, Boundary Layer Meteorol., 60, 375-395.

Pulliam, T. H. & Steger, J. L. 1980  Implicit Finite-Difference Simulations of three-dimensional Compressible Flow, AIAA Journal 18, 2, 159.

Rotta, J.C. 1972 Turbulente Stromungen. Eine Einfuhrung in die Theorie und ihre Anwendung. B. G. Teubner Stuttgart. P. 156.

Sams, E.W. 1952 Experimental investigation of average heat transfer and friction coefficients for air flowing in circular tubes having square-thread-type roughness. NACA RME 52 D 17.

Savage, D.W. & Myers, J.E. 1963 The effect of artificial surface roughness on heat and momentum transfer. A.I.Ch.E.J., 9, 694-702.

Schlichting, H. 1936 Experimentelle Untersuchungen zum Rauhigkeits-problem. Ing.-Arch 7(1), 1-34.

Schlichting, H. 1960 Boundary Layer Theory. McGraw-Hill, NY, p.527.

Sheriff, N., Gumley, P. & France, J. 1963 Heat transfer characteristics of roughened surfaces. UKAEA, TRG Report 447 (R). 

Sigal, A & Danberg, J.E. 1990 New Correlation of Roughness Density Effect on the Turbulent Boundary Layer.  AIAA Journal, 25, 3, 554-556.

Simpson, R. L. 1973 A Generalized Correlation of Roughness Density Effect on the Turbulent Boundary Layer. AIAA Journal 11, 9,  242-244.

Skupinski, E. 1961 Wärmeübergang und Druckverlust bei künstlicher Verwirbelung und künstlicher Wandrauhigkeiten. Diss. Techn. Hochschule Aachen.

Smith, R.W. 1994 Effect of Reynolds Number on the Structure of Turbulent Boundary Layers. Ph.D. Thesis, Princeton University, Princeton, NJ.

Stephens, M. J. 1970 Investigations of flow in a concentric annulus with smooth outer wall and rough inner wall. CEGB RD/B/N 1535, Berkley Nuclear Laboratories.

Trunev, A. P. 1995 Diffuse processed in turbulent boundary layer over rough surface. In Air Pollution III, Theory and Simulation (ed. H. Power, N. Moussiopoulos & C.A. Brebbia). Comp. Mech. Pub. Southampton-Boston.

Trunev, A. P. 1996 Similarity theory for turbulent flow over natural rough surface in pressure and temperature gradients. In Air Pollution IV, Monitoring, Simulation and Control, (ed. B. Caussade, H. Power & C.A. Brebbia ).Comp. Mech. Pub. Southampton-Boston.

Trunev, A. P. 1997 Similarity theory and model of diffusion in turbulent atmosphere at large scales. In Air Pollution V, Modelling, Monitoring and Management. (ed. H. Power, T. Tirabassi & C .A. Brebbia) Comp. Mech. Pub. Southampton-Boston.

Trunev, A. P. & Fomin, V.M. 1985 Continual model of impingement erosion. J. Appl. Mech. and Tech. Phys., 6, pp. 113-120. 

Watson, M.A.P. 1970 The performance of a square rib type of heat transfer surface. CEGB RD/B/N  1738, Berkeley Nuclear Laboratories.

Webb, R. L., Eckert, E.R.G. & Goldstein, R. J. 1971 Heat transfer and friction in tubes with repeated-rib roughness. Int. J. Heat Mass Transfer, 14, 601-617.

Wieringa, J. 1992 Updating the Davenport Roughness Clarification. J. Wind Engineer. Industl. Aerodyn. 41, 357–368.